이 글은 원 저자들의 허락하에 번역되어 게재 되었습니다. 이 글의 원문은 여기에서 다운 받을 수 있습니다.

딥 러닝을 위한 콘볼루션 계산 가이드

Vincent Dumoulin(MILA, 몬트리올 대학), Francesco Visin(AIRLab, 밀라노 공과대학)

2016년 4월 24일

감사의 말

유용한 피드백을 보내 준 David Warde-Farley, Guillaume Alain 그리고 Caglar Culcehre에게 감사합니다.

특별히 이 문서의 그림에서 사용된 색깔인 Solarized 컬러 스킴을 만든 Ethan Schoonover에게 감사드립니다.

피드백

피드백은 언제든지 환영합니다! 가능한 정확하고 상세하게 기술하려고 최선을 다했지만 혹 잘못된 점을 발견했거나 설명을 바꿀 필요가 있거나 좀 더 상세히 할 부분이 있다면 주저하지 말고 연락 주세요. 마찬가지로 이 리포트에 어울리는 뭔가가 있거나 우리와 논의할 게 있다면 연락 주세요. 최선을 다해 이 문서를 업데이트하도록 하겠습니다.

소스코드와 이미지

그림과 함께 이 문서를 만든 코드는 깃허브에 공개되어 있습니다. 그리고 이 문서에 있는 이미지의 애니메이션 버전도 있습니다.

1장. 소개

딥 콘볼루션 뉴럴 네트워크(Deep Convolutional Neural Networks, CNNs)는 딥 러닝 분야에서 일어난 놀라운 발전의 핵심입니다. CNNs은 글자 인식 문제를 풀기위해(Le Cun 외, 1997) 90년대 이미 사용되었지만 현재처럼 널리 쓰이게 된 것은 최근의 연구 결과 덕택입니다. 그리고 딥 CNN은 ImageNet 이미지 분류 시합에서 다른 경쟁자들을 이기고 우승을 차지했습니다(Krizhevsky 외, 2012)

이제 콘볼루션 뉴럴 네트워크는 머신러닝 분야애서 매우 유용한 툴이 되었습니다. 하지만 처음 CNNs을 배우는 것은 그리 쉽지만은 않습니다. 콘볼루션 레이어(layer)의 출력(output) 크기는 입력(input)의 크기와 커널(kernel) 크기의 선택, 제로 패딩(padding), 스트라이드(stride) 등에 영향을 받습니다. 이러한 요소간의 상호관계는 쉽게 짐작하기 어렵습니다. 이 부분이 출력 크기가 입력 크기와 상관이 없는 완전 연결(fully-connected) 뉴럴 네트워크와 대비되는 점입니다. 추가적으로 CNNs은 풀링(pooling)이라는 단계를 가지고 있어 완전 연결 뉴럴 네트워크에 비해 좀 더 복잡해 집니다. 마지막으로 전치 콘볼루션 레이어(또는 부분 스트라이드 콘볼루션 레이어라고 알려진)는 최근에 점점 많은 곳에서 채택되고 있고(Zeiler 외, 2011; Zeiler and Fergus, 2014; Long 외, 2015; Rad-ford 외, 2015; Visin 외, 2015; Im 외, 2016) 콘볼루션 레이어와의 관계가 여러 관점에서 설명되어 왔습니다.

(역주: 전치 콘볼루션은 초기에 디콘볼루션[deconvolution]이라고 불리웠는데 보다 명확한 의미 전달을 위해 전치 콘볼루션으로 바뀌고 있는 것으로 보입니다. 텐서플로우에도 같은 역할을 하는 conv2d_transpose 함수가 있습니다.)

이 가이드의 목적은 두가지 입니다.

콘볼루션 레이어와 전치 콘볼루션 레이어간의 관계를 설명합니다.
콘볼루션 레이어와 전치 콘볼루션 레이어에서 입력 크기, 커널 크기, 제로 패딩, 풀링, 스트라이드 그리고 출력 크기 간의 관계를 알기 쉽게 설명합니다.

폭 넓게 적용될 수 있도록 이 가이드에서 제시한 결과는 특정 구현에 종속되어 있지 않으며 대부분의 머신러닝 프레임워크, 예를 들면 씨아노(Theano. Bergstra 외, 2010; Bastien 외, 2012), 토치(Torch. Collobert 외, 2011), 텐서플로우(TensoFlow. Abadi 외, 2015), 카페(Caffe. Jia 외, 2014) 등에 적용할 수 있습니다.

이 장에서는 CNNs의 분할 콘볼루션, 풀링 같은 주요 구성 요소에 대해 간략히 살펴 보겠습니다. 이 주제에 대한 심도 깊은 자료는 딥 러닝 책(Goodfellow 외, 2016) 9장을 참고하세요.

1.1 분할 콘볼루션(Discrete convolutions)

(역주: 이 문서에서 말하는 Discrete convolution이 보통 우리가 말하는 일반적인 콘볼루션입니다. discrete란 단어가 흔히 ‘이산’으로 번역되지만 오히려 더 어렵게 느껴지는 것 같아 분할 콘볼루션이라고 적었습니다. 입력값의 축 방향을 따라 조금씩 나뉘어 콘볼루션 된다는 의미로 해석할 수 있습니다.)

뉴럴 네트워크의 기본 요소는 아핀 변환(affine transformation)입니다. 한 벡터를 입력으로 받아서 한 행렬을 곱하여 출력을 만듭니다(보통 비선형적으로 변환하기 전에 편향[bias] 벡터를 더합니다). 이미지나 사운드 클립 또는 순서가 없는 속성을 가진 데이터라면 어떠한 종류의 입력에도 적용될 수 있습니다. 그들의 차원이 어떻든 간에 변환하기 전에 하나의 벡터로 직렬화 시킬 수 있기 때문입니다.

이미지, 사운드 클립 그리고 유사한 종류의 많은 데이터들이 고유한 구조를 가지고 있습니다. 구체적으로 말하면 이런 데이터는 다음과 같은 중요한 성질을 가집니다.

다차원 배열로 저장됩니다.
순서가 있는 하나 이상의 축을 가집니다(예를 들면 이미지의 폭이나 높이 방향의 축, 사운드 클립의 시간축).
채널이라 불리는 축은 데이터를 다른 관점으로 보는데 사용됩니다(예를 들면 컬러 이미지의 적, 녹, 청 채널이나 스테레오 오디오 트랙의 좌우 채널)

이런 성질들은 아핀 변환을 할 때 이용되지 않습니다. 사실 모든 축이 같은 방식으로 처리되므로 구조적인 정보는 고려되지 않습니다. 하지만 데이터에 내재된 구조를 이용하는 것이 컴퓨터 비전이나 음성인식 같은 분야의 문제들을 해결하는데 유리하다고 알려져 있습니다. 이런 경우엔 구조적 정보를 유지하는 것이 최선입니다. 그래서 분할 콘볼루션이 등장하게 되었습니다.

분할 콘볼루션은 순서 정보를 유지한 선형변환입니다. 이는 데이터를 부분부분 잘라 사용하고(하나의 출력 요소를 만들기 위해 몇개의 입력 요소만 사용되므로) 파라메타를 재 사용합니다(같은 가중치 값이 입력 데이터의 여러 위치에 적용되므로).

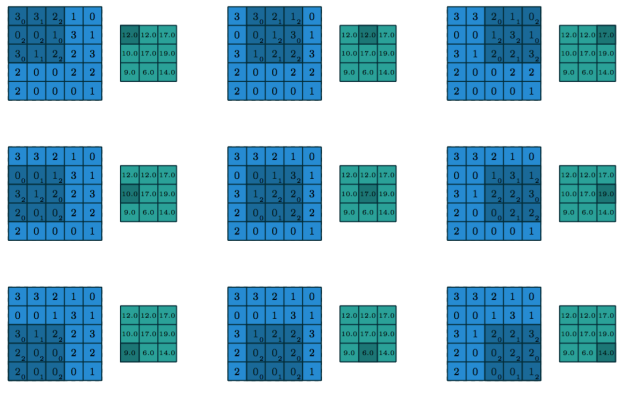
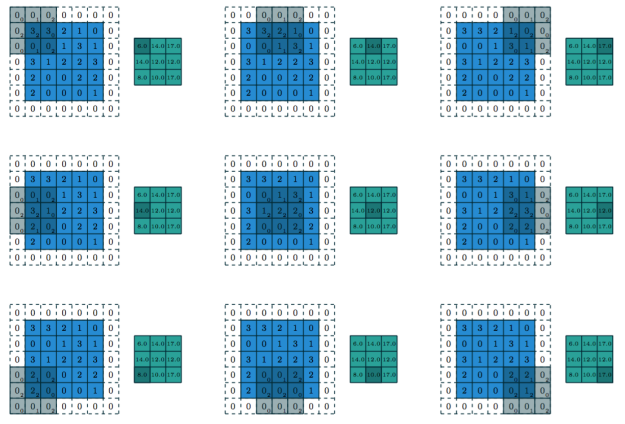
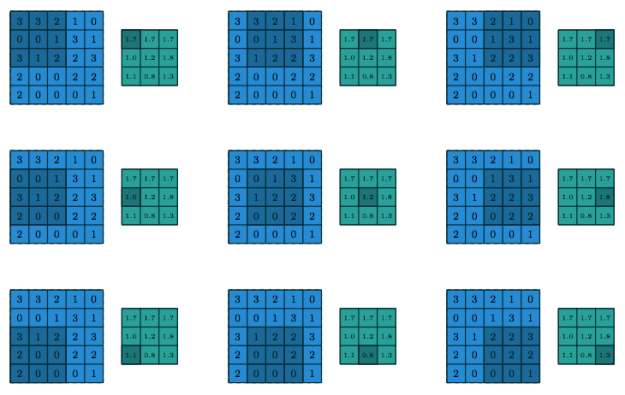
그림 1.1은 분할 콘볼루션의 예를 보여줍니다. 밝은 파랑색 격자를 입력 특성 맵(input feature map)이라고 부릅니다. 간단하게 나타내려고 하나의 특성 맵만 그렸지만 여러개의 특성 맵을 쌓아 올려져 있는 것이 일반적입니다(앞서 언급한 이미지나 사운드 클립의 채널이 좋은 예입니다). 커널(어두운 부분)이 입력 특성 맵을 슬라이딩하여 지나갑니다. 각 위치마다 커널의 원소와 오버랩되는 입력 원소가 곱해져서 그 합이 현재 위치의 출력 값이 됩니다. 이런 과정은 출력 특성 맵을 구성하는데 필요한 만큼 다른 커널을 사용하여 반복될 수 있습니다(그림 1.3). 최종 출력을 출력 특성 맵(output feature map)이라고 부릅니다(시그널 프로세싱 측면에서 보면 콘볼루션과 크로스 코릴레이션[cross-correlation] 사이에 차이가 있지만 커널을 학습시킬 때는 큰 차이가 없습니다. 심플하기도 하고 대부분의 머신러닝 자료들과 일관성을 유지하기 위해서 이 가이드에서는 콘볼루션이란 용어를 사용합니다). 여러개의 입력 특성 맵이 있는 경우엔 커널은 3차원 형태를 띠게 됩니다. 각각의 입력 특성 맵 하나가 하나의 커널에 콘볼루션 되어 계산된 특성 맵을 원소별로 더해 출력 특성 맵을 만듭니다.

그림 1.1: 분할 콘볼루션의 출력값 계산

그림 1.1에 묘사된 콘볼루션은 2-D 콘볼루션의 예입니다. 하지만 이는 N-D 콘볼루션으로 일반화시킬 수 있습니다. 예를 들면 3-D 콘볼루션에서는 커널은 직육면체가 되며 입력 특성 맵의 높이, 넓이 그리고 깊이를 따라 슬라이드 하게 됩니다.

분할 콘볼루션을 정의하는 커널들은 아래 치환기호( $n$ , $m$ , $k_1$ ~ $k_m$ )에 상응하는 크기를 가집니다.

$n \equiv$ 출력 특성 맵의 갯수
$m \equiv$ 입력 특성 맵의 갯수
$k_j \equiv$ $j$ 축 방향의 커널 크기

어떤 콘볼루션 레이어의 $j$ 축 방향의 출력 사이즈 $o_j$ 에 영향을 미치는 속성은 다음과 같습니다.

$i_j$ : $j$ 축 방향의 입력 사이즈
$k_j$ : $j$ 축 방향의 커널 사이즈
$s_j$ : $j$ 축 방향의 스트라이드 (커널의 연속적인 두 위치 사이의 거리)
$p_j$ : $j$ 축 방향의 제로 패딩 (축의 시작과 끝에 추가되는 0의 갯수)

예를 들어 그림 1.2는 1×1 제로 패딩된 5×5 입력에 2×2 스트라이드로 3×3 커널이 적용되는 예입니다.

그림 1.2: $N$ = 2, $i_1$ = $i_2$ = 5, $k_1$ = $k_2$ = 3, $s_1$ = $s_2$ = 2 그리고 $p_1$ = $p_2$ = 1 일 때 분할 콘볼루션의 출력값 계산

스트라이드는 서브 샘플링(subsampling)과 같은 모습을 만들어 줍니다. 스트라이드는 커널이 한번에 얼마나 많이 이동하는지로 설명하기도 하지만 출력이 얼마나 많이 남아있는지로 표현할 수도 있습니다. 예를 들면 두개씩 건너서 커널을 움직이는 것은 한칸씩 커널을 움직이되 홀수개의 출력만 취하는 것과 동일합니다(그림 1.4).

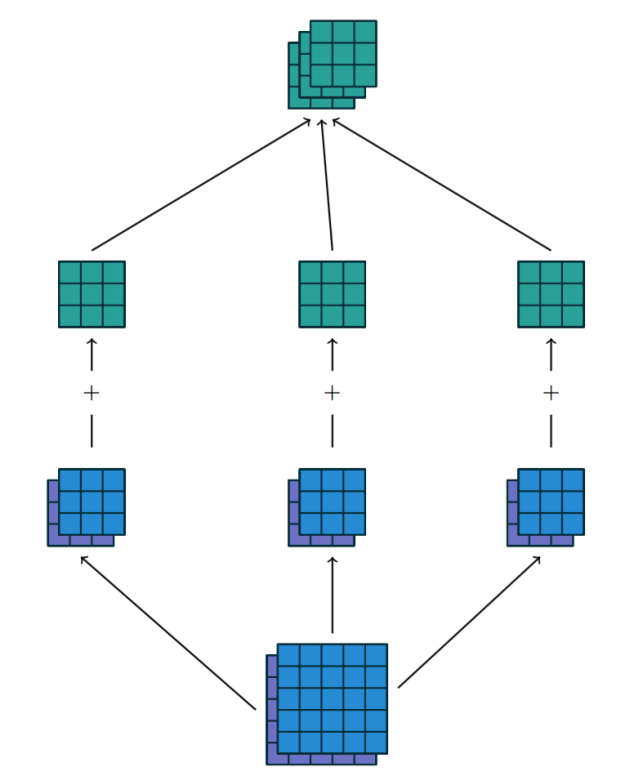
그림 1.3: 3x2x3x3 커널 $w$ 를 사용한 두개의 입력 특성 맵에서 세개의 출력 특성 맵으로의 콘볼루션 매핑. 맨 왼쪽부터 입력 특성 맵 1 은 커널 $w_{1,1}$ 에 콘볼루션 되고 입력 특성 맵 2 는 커널 $w_{1,2}$ 에 콘볼루션 되어 그 계산 결과는 요소별로 더해져서 첫번째 출력 특성 맵을 만듭니다. 같은 방식으로 가운데와 오른쪽에 적용되어 두번째 세번째 특성 맵이 구성됩니다. 세개의 출력 특성 맵은 하나로 묶여져 최종 출력 값이 됩니다.

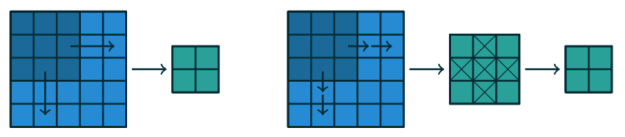
그림 1.4: 스트라이드를 바라보는 다른 관점. s = 2 씩 증가하는 3×3 커널로 생각하는 대신(왼쪽), 1씩 증가하되 s = 2인 출력만 취하는 것으로 볼 수 있음(오른쪽)

1.2 풀링(Pooling)

분할 콘볼루션과 함께 풀링 연산은 CNNs의 중요한 구성요소 중 하나입니다. 풀링 연산은 평균을 내거나 최대값을 선택하는 함수를 사용하여 영역의 일부분을 압축하여 특성 맵의 크기를 줄여 줍니다.

풀링은 윈도우를 입력 값 위로 슬라이딩하면서 윈도우에 나타나는 값을 풀링 함수에 입력하는 방식으로 작동합니다. 어떤 면에서는 풀링은 분할 콘볼루션과 매우 비슷하게 작동합니다. 하지만 풀링의 다른 점은 커널과의 션형 계산을 다른 종류의 함수로 바꾼 것입니다. 그림 1.5는 평균 풀링의 예를 나타내고 그림 1.6은 맥스 풀링의 예입니다.

다음은 풀링 레이어의 $j$ 축 방향의 출력 사이즈 $o_j$ 에 영향을 미치는 요소입니다.

$i_j$ : $j$ 축 방향의 입력 크기
$k_j$ : $j$ 축 방향의 풀링 윈도우 크기
$s_j$ : $j$ 축 방향의 스트라이드 (연속된 풀링 윈도우 위치 간의 거리)

그림 1.5: 5×5 입력에 1×1 스트라이드로 3×3 평균 풀링 연산의 출력값 계산

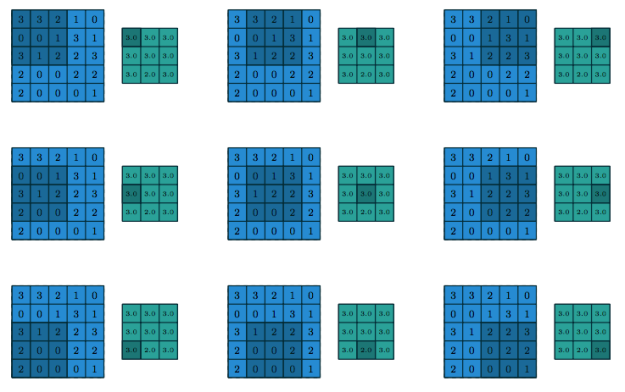
그림 1.6: 5×5 입력에 대해 1×1 스트라이드로 3×3 맥스 풀링 연산의 출력값 계산

2장. 콘볼루션 계산

콘볼루션 레이어의 속성 간의 관계는 서로 다른 축끼리는 영향을 끼치지 않는다는 사실을 알면 쉽게 이해할 수 있습니다. 예를 들면 $j$ 축 방향의 커널 크기, 제로 패딩, 스트라이드는 $j$ 축 방향의 출력에만 영향을 미칩니다. 그렇기 때문에 이 장에서는 다음과 같이 문제를 단순화하여 진행합니다.

2-D 분할 콘볼루션 ( $N = 2$ )
정방형 입력 ( $i_1 = i_2 = i$ )
정방형 커널 ( $k_1 = k_2 = k$ )
두 축 방향으로 동일한 스트라이드 ( $s_1 = s_2 = s$ )
두 축 방향으로 동일한 제로 패딩 ( $p_1 = p_2 = p$ )

이런 설정은 분석과 시각화를 쉽게 만들어 줍니다. 하지만 이 문서의 내용은 N-D 차원과 정방향이 아닌 경우로 확장할 수 있다는 것을 기억하세요.

2.1 제로 패딩 없음, 단일 스트라이드

분석하기에 가장 간단한 경우는 커널이 입력의 모든 위치를 슬라이딩할 때입니다(즉 $s = 1$ 그리고 $p = 0$ ). 그림 2.1은 $i = 4$ 이고 $k = 3$ 일 때의 예입니다.(역주: 깃허브의 애니메이션 버전이 있는 경우 페이퍼의 그림 대신 사용했습니다.)

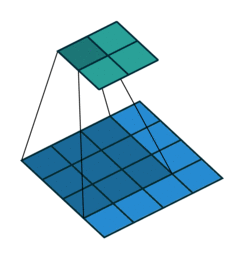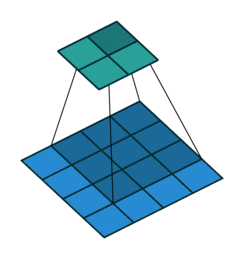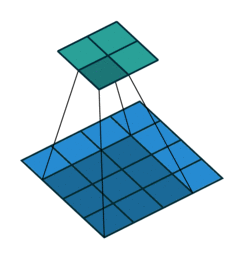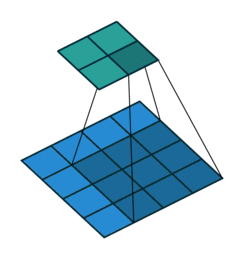
그림 2.1: (패딩 없음, 단일 스트라이드) 4×4 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션 하기 (i = 4, k = 3, s = 1 그리고 p = 0)

이 경우에 커널이 입력위에 놓일 수 있는 횟수로 출력의 크기를 정의할 수 있습니다. 폭 방향의 축을 생각해 보면 커널은 입력 특성 맵의 가장 왼쪽에서 시작해서 입력의 오른쪽 끝을 만날 때까지 한 스텝씩 지나갑니다. 출력의 크기는 커널이 이동하는 스텝 수에 초기 위치(그림 2.8a)를 반영하여 1을 더한 값입니다. 동일한 로직이 높이 방향으로도 적용됩니다.

이를 수식으로 나타내면 아래와 같이 쓸 수 있습니다.

식 1. 임의의 $i$ 와 $k$ 에 대해 $s = 1$ 그리고 $p = 0$ 일 때,

$o = (i - k) + 1$

(역주: 이 식은 가장 일반화된 식 6에 $p = 0$ , $s = 1$ 을 대입한 것과 동일합니다)

2.2 제로 패딩, 단일 스트라이드

제로 패딩 측면에서(즉 $s = 1$ 이라고만 가정하고) 콘볼루션 되는 실제 입력 사이즈가 어떻게 영향을 받는지 생각해 봅시다. $p$ 개의 제로 패딩은 입력 사이즈 $i$ 를 $i + 2p$ 로 바꿉니다. 일반적으로 쓰면 식 1을 사용하여 다음과 같은 식을 유도할 수 있습니다.

식 2. 임의의 $i$ , $k$ 와 $p$ 에 대해 $s = 1$ 일 때,

$o = (i - k) + 2p + 1$

(역주: 이 식은 가장 일반화된 식 6에 $s = 1$ 을 대입한 것과 동일합니다)

그림 2.2는 $i = 5$ , $k = 4$ , $p = 2$ 일 때 예입니다.

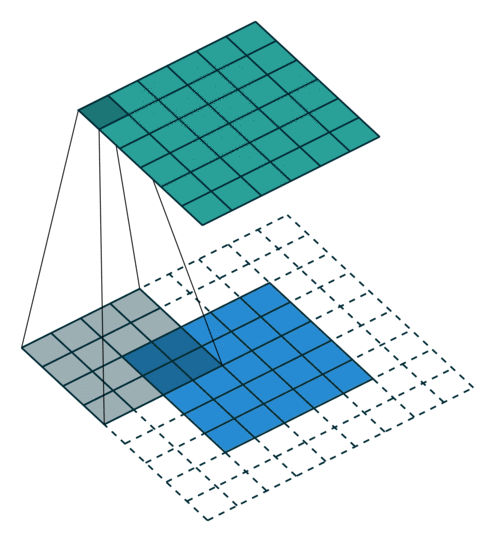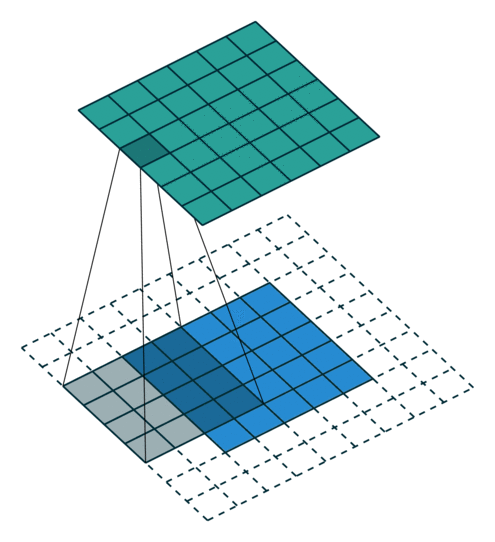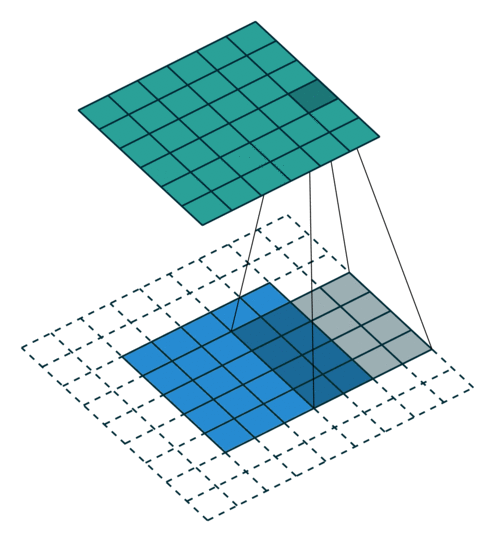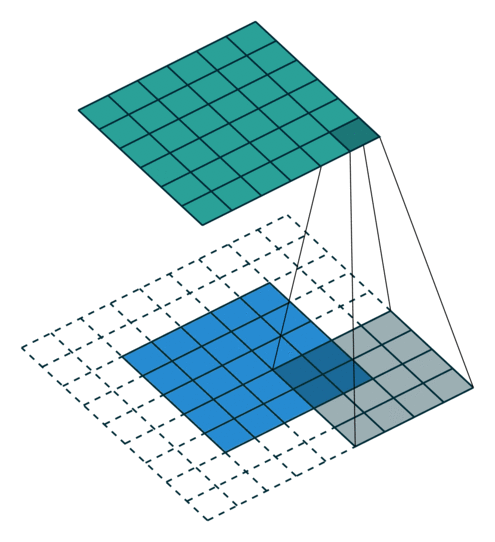
그림 2.2: (임의의 패딩, 단일 스트라이드) 2×2 제로 패딩된 5×5 입력에 대해 단일 스트라이드로 4×4 커널을 콘볼루션하기 (즉 i = 5, k = 4, s = 1 그리고 p = 2)

실제로는 특별한 성질을 가지고 있는 제로 패딩의 전형적인 두가지 케이스가 아주 널리 사용됩니다. 이 두가지를 자세히 살펴 보겠습니다.

2.2.1 하프(half, 또는 동일) 패딩

출력 크기를 입력 크기와 동일하게(즉 $o = i$ ) 만들어야 할 때가 있습니다.

식 3. 임의의 $i$ 에 대해 $k$ 가 홀수( $k = 2n + 1$ , $n \in N$ ), $s = 1$ , $p = \lfloor \dfrac{k}{2} \rfloor = n$ 일 때,

$o = i + 2p - k + 1 = i + 2 \lfloor \dfrac{k}{2} \rfloor - (k - 1) = i + 2n - 2n = i$

(역주: 텐서플로우에서는 conv2d 함수에 스트라이드를 1 로 하고 padding 옵션에 ‘SAME’ 을 사용합니다)

이를 종종 하프(또는 동일) 패딩이라고 부릅니다. 그림 2.3은 $i = 5$ , $k = 3$ 그러므로 $p = 1$ 인 예입니다.

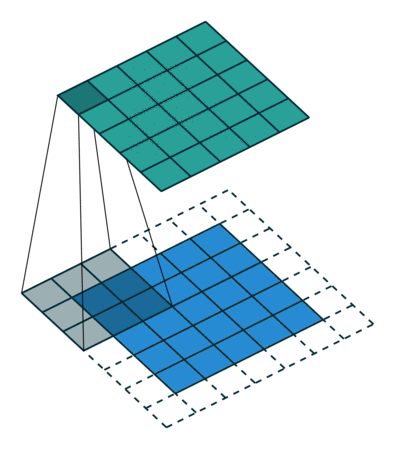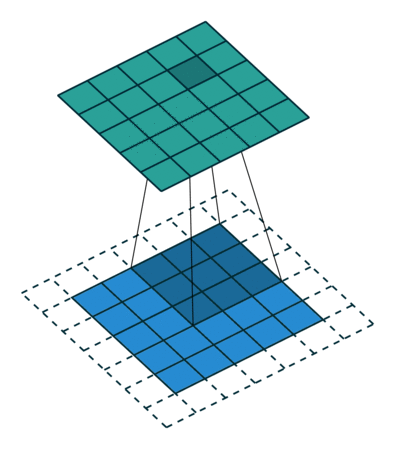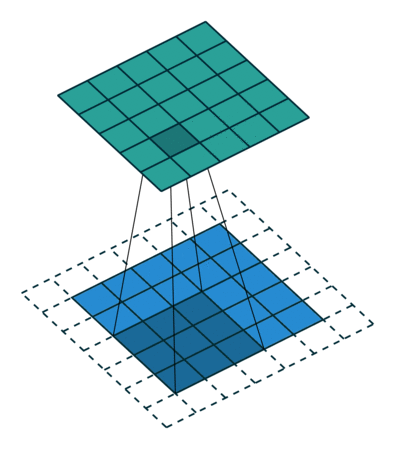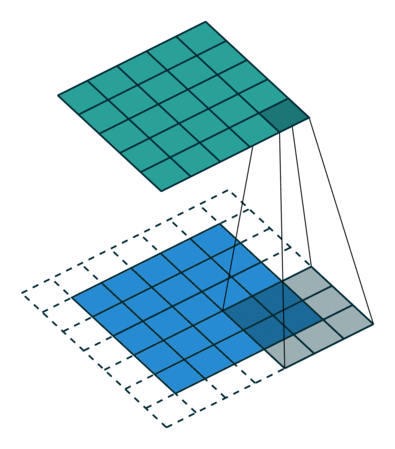
그림 2.3: (하프 패딩, 단일 스트라이드) 하프 패딩된 5×5 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션 하기 (즉 i = 5, k = 3, s = 1 그리고 p = 1)

2.2.2 풀(full) 패딩

커널을 콘볼루션 하면 보통 입력 크기 보다 출력 크기가 줄어 들지만 가끔은 그 반대의 경우가 필요할 때가 있습니다. 적절한 패딩을 넣으면 이렇게 만들 수 있습니다.

식 4. 임의의 $i$ 와 $k$ 에 대해 $p = k - 1$ , $s = 1$ 일 때,

$o = i + 2(k - 1) - (k - 1) = i + (k - 1)$

이렇게 하면 커널이 입력 특성 맵에 부분적이든지 완전 겹치든지 가능한 모든 경우가 고려되기 때문에 이를 종종 풀 패딩이라고 부릅니다. 그림 2.4는 $i = 5$ , $k = 3$ 그러므로 $p = 2$ 인 예입니다.

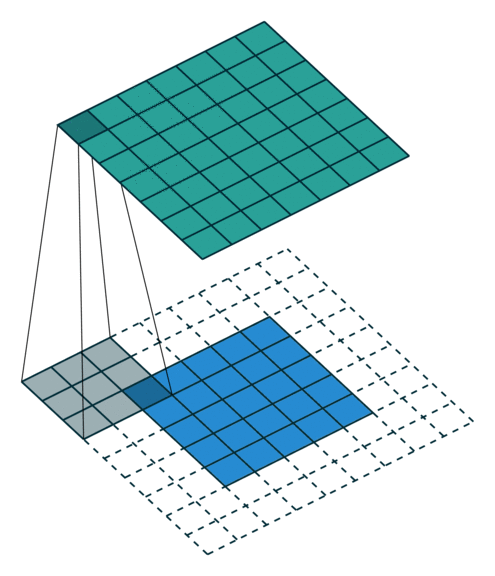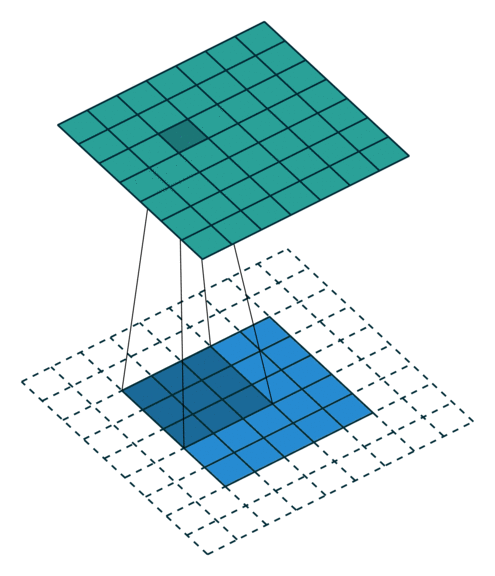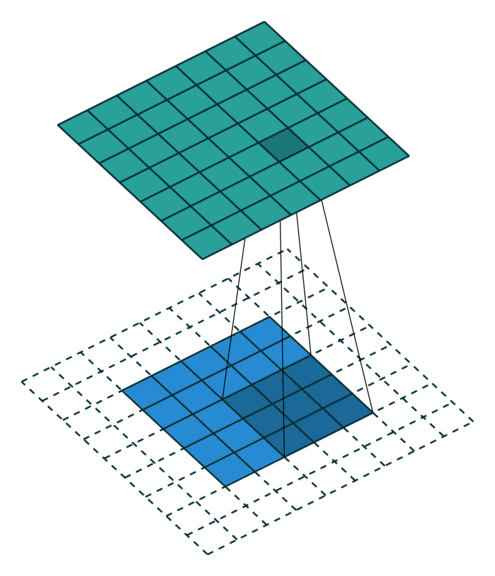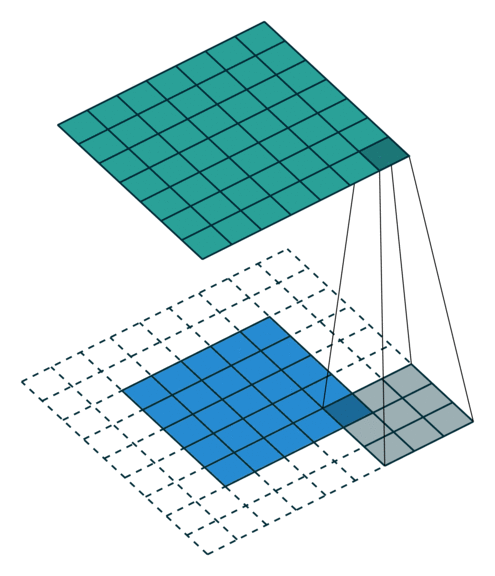
그림 2.4: (풀 패딩, 단일 스트라이드) 풀 패딩된 5×5 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션하기 (즉 i = 5, k = 3, s = 1 그리고 p = 2)

2.3 제로 패딩 없음, 다중 스트라이드

이제까지 유도된 모든 식은 단일 스트라이드 콘볼루션에 대해서만 적용되는 것입니다. 다중 스트라이드를 다루기 위해서는 추가적으로 고려해야할 것이 있습니다. 분석을 쉽게 하기 위해 잠시 제로 패딩은 무시하도록 합니다(즉 $s > 1$ 이고 $p = 0$ ). 그림 2.5는 $i = 5$ , $k = 3$ , $s = 2$ 인 예입니다.

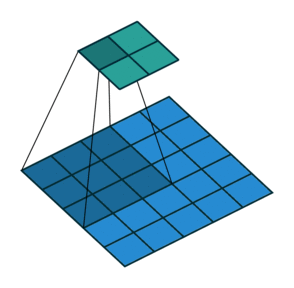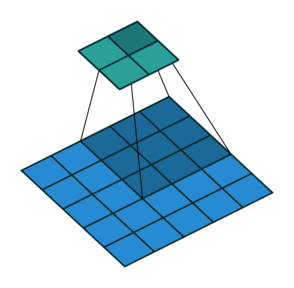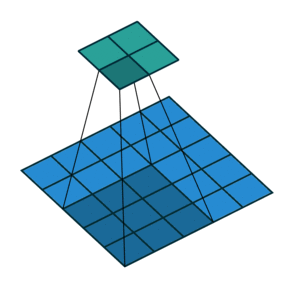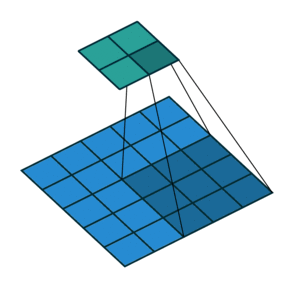
그림 2.5: (제로 패딩 없음, 임의의 스트라이드) 5×5 입력에 2×2 스트라이드로 3×3 커널을 콘볼루션 하기 (즉 i = 5, k = 3, s = 2 그리고 p = 0)

여기서도 마찬가지로 출력 사이즈는 입력 위에 커널이 놓일 수 있는 횟수로 정의할 수 있습니다. 폭 방향을 먼저 보면 커널은 입력의 왼쪽 끝 부터 시작합니다. 하지만 이번엔 $s$ 만큼 보폭으로 입력의 오른쪽 끝까지 슬라이드 합니다. 출력 크키는 커널의 초기 위치를 반영하여 스텝 수에 1을 더한 값이 됩니다(그림 2.8b). 같은 방법으로 높이 방향 축에 적용합니다.

이것으로 부터 다음 식이 유도될 수 있습니다.

식 5. 임의의 $i$ , $k$ 그리고 $s$ 에 대해 $p = 0$ 일 때,

$o = \lfloor \dfrac{i - k}{s} \rfloor + 1$

(역주: 이 식은 가장 일반화된 식 6에 $p = 0$ 을 대입한 것과 동일합니다)

내림(floor) 함수가 적용되는 것은 커널의 마지막 스텝이 입력의 끝과 맞지 않는 경우가 있기 때문입니다. 즉 일부 입력 원소는 버려지게 됩니다(그림 2.7이 이런 경우의 예입니다).

(역주: 텐서플로우에서는 conv2d 함수에 padding 옵션에 ‘VALID’ 을 사용합니다)

2.4 제로 패딩, 다중 스트라이드

가장 일반적인 케이스(제로 패딩이 된 입력에 다중 스트라이드로 콘볼루션 하는 것)를 식 2에서 했던 것 처럼 식 5에서 실제 입력 사이즈를 $i + 2p$ 로 대체 함으로써 유도할 수 있습니다.

식 6. 임의의 $i$ , $k$ , $p$ 그리고 $s$ 에 대해,

$o = \lfloor \dfrac{i + 2p - k}{s} \rfloor + 1$

(역주: 텐서플로우에서는 임의의 패딩 옵션으로 콘볼루션 하려면 tf.pad 함수를 사용하여 직접 패딩을 추가한 후에 conv2d 함수를 ‘VALID’ 패딩 옵션으로 사용해야 합니다)

위에서와 같이 내림(floor) 함수는 다른 크기의 입력에 대해 콘볼루션할 때 같은 출력 크기를 만들어 낼 수 있다는 걸 의미합니다. 구체적인 예를 보면, $i + 2p - k$ 가 $s$ 의 배수일 경우 입력 크기 $j = i + a$ , $a \in {0, ..., s-1}$ 은 같은 출력 크기를 만듭니다. 이런 동작은 $s > 1$ 일 때만 해당됩니다.

그림 2.6은 $i = 5$ , $k = 3$ , $s = 2$ 그리고 $p = 1$ 일 때의 예를 보여주고 그림 2.7은 $i = 6$ , $k = 3$ , $s = 2$ 그리고 $p = 1$ 일 때의 예입니다. 서로 다른 입력 크기를 가지고 있음에도 같은 출력 사이즈로 콘볼루션 됩니다. 이런 현상이 콘볼루션 분석에는 영향을 미치지 않지만 전치 콘볼루션의 경우에는 분석을 복잡하게 만듭니다.

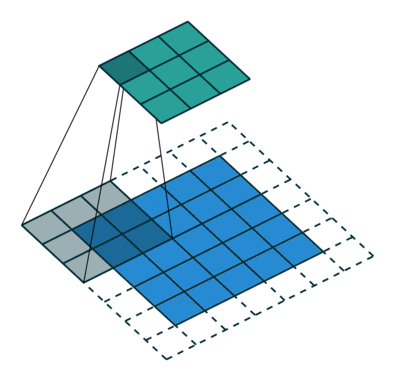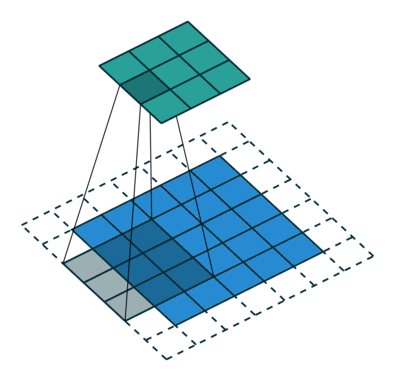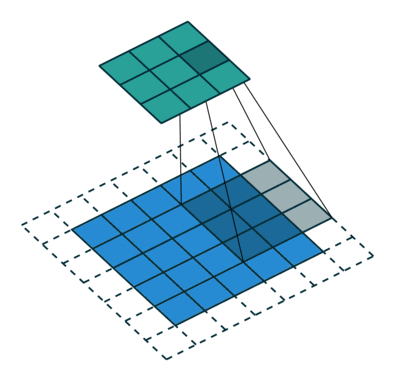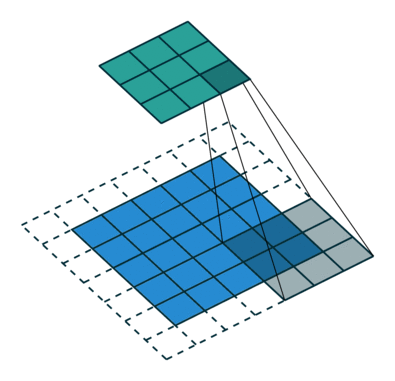
그림 2.6: (임의의 패딩, 임의의 스트라이드) 테두리가 1×1 크기로 제로 패딩된 5×5 입력에 2×2 스트라이드로 3×3 커널을 콘볼루션하기 (즉 i = 5, k = 3, s = 2 그리고 p = 1)

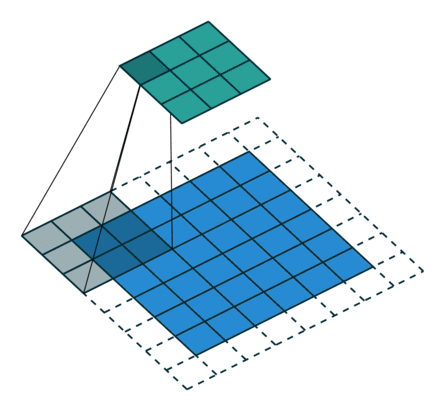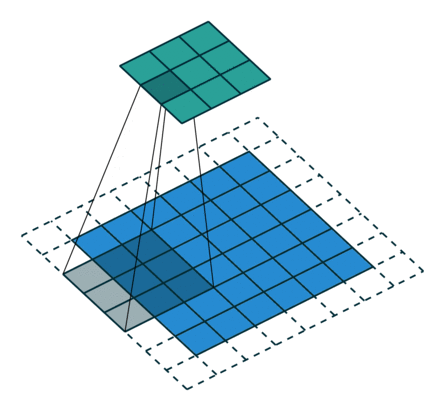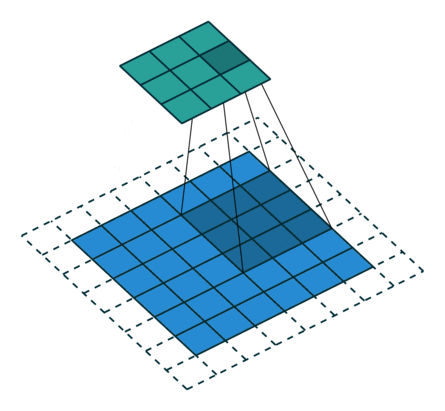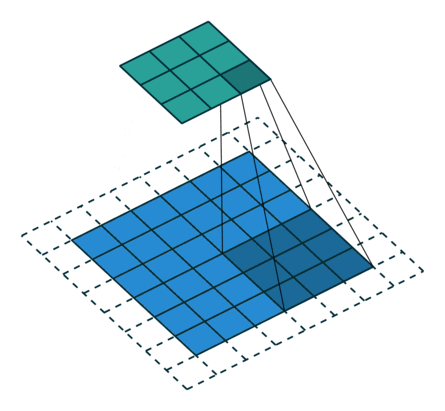
그림 2.7: (임의의 패딩, 임의의 스트라이드) 테두리가 1×1 크기로 제로 패딩된 6×6 입력에 2×2 스트라이드로 3×3 커널을 콘볼루션 하기(즉 i = 6, k = 3, s = 2 그리고 p = 1). 이 경우 제로 패딩된 맨 아래 행과 가장 오른쪽 열은 커널에 콘볼루션되지 않습니다.

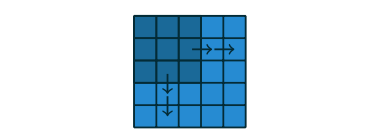
그림 2.8: 커널 위치 카운팅. (a) 이 커널은 오른쪽으로 두번 이동하면 입력의 오른쪽 끝에 다다릅니다(아래 방향도 마찬가지 입니다). 초기 커널 위치를 고려해 1을 더하면 출력은 3×3 크기가 됩니다.

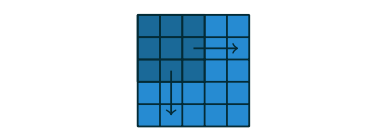
그림 2.8: 커널 위치 카운팅. (b) 이 커널은 오른쪽으로 두칸씩 한번만 이동하면 입력의 오른쪽 끝에 다다릅니다(아래 방향도 마찬가지 입니다). 초기 커널 위치를 고려해 1을 더하면 출력은 2×2 크기가 됩니다.

3장. 풀링(Pooling) 계산

풀링 레이어는 뉴럴 네트워크가 입력의 작은 변화에 민감하지 않도록 만들어 줍니다. 가장 널리 사용되는 풀링은 입력을 조각으로 나누어(일반적으로 겹쳐지지 않도록) 각 조각에서 가장 큰 값을 취하는 맥스 풀링(max pooling) 입니다. 다른 종류의 풀링으로는 중간값(mean) 또는 평균값 풀링 입니다. 이들은 모두 조각안의 값들에 비선형성을 부여하는 것으로써 입력 값을 부분 부분 합친다는 동일한 아이디어를 바탕으로 합니다(Boureau 외, 2010a, b, 2011; Saxe 외, 2011).

콘볼루션 계산이 어떤 함수가 입력의 부분 부분에 반복적으로 적용된다는 가정을 바탕으로 한다는 것을 눈치 챘을 지 모르겠습니다. 이 말은 앞장에서 유도한 식을 풀링 계산에서도 재 사용할 수 있다는 뜻입니다. 풀링은 제로 패딩을 가지지 않으므로 일반적인 경우의 식은 아래와 같습니다.

식 7. 임의의 $i$ , $k$ 그리고 $s$ 일 때,

$o = \lfloor \dfrac{i - k}{s} \rfloor + 1$

이 식은 어떤 종류의 풀링에도 적용됩니다.

4장. 전치(transposed) 콘볼루션 계산

일반적인 콘볼루션의 반대 방향으로 콘볼루션을 하고자 할 때 전치 콘볼루션이 필요합니다. 즉 어떤 콘볼루션의 출력 크기에서 연결 패턴을 유지한 채 그 콘볼루션의 입력 크기로 변환하는 것입니다. 예를 들면 콘볼루션 오토인코더(autoencoder)의 디코딩(decoding) 레이어나 특성 맵을 고차원 공간(higher-dimensional space)으로 프로젝션 시키기 위해 이런 변환을 사용할 수 있습니다.

(역주: 연결 패턴을 그대로 유지한다는 것은 입력과 출력의 원소간 대응 관계를 같게 한다는 뜻 입니다)

전치된 가중치 행렬 하나만 필요한 이 콘볼루션도 완전 연결(fully-connected)의 경우보다 더 복잡니다. 그러나 어떤 콘볼루션도 효율적인 행렬 연산으로 축약시킬 수 있으므로 완전 연결의 경우에서 얻은 통찰은 이 콘볼루션의 경우에도 유용합니다.

콘볼루션 계산처럼 전치 콘볼루션 계산에 관한 논증은 다른 축끼리는 서로 영향을 끼치지 않는다는 점을 이용해 간소화시킬 수 있습니다.

이 장에서는 아래 가정하에서 진행합니다.

2-D 전치 콘볼루션 ( $N = 2$ )
정방향 입력 ( $i_1 = i_2 = i$ )
정방향 커널 크기 ( $k_1 = k_2 = k$ )
각 축 방향으로 동일한 스트라이드 ( $s_1 = s_2 = s$ )
각 축 방향으로 동일한 제로 패딩 ( $p_1 = p_2 = p$ )

여기에서도 서술된 결과는 N-D 차원과 정방형이 아닌 경우로 일반화될 수 있습니다.

4.1 행렬 연산으로 표현한 콘볼루션

그림 2.1의 콘볼루션을 예로 들어 보겠습니다. 입력과 출력의 원소를 왼쪽에서부터 오른쪽으로 그리고 위에서 아래로 벡터로 풀어 놓으면 콘볼루션은 0이 아닌 원소를 커널의 $w_{ij}$ 원소( $i$ 와 $j$ 는 각각 커널의 행과 열입니다)로 나타낸 희소(sparse) 행렬 $C$ 로 나타낼 수 있습니다.(역주: 즉 이 행렬의 행은 커널의 한 스텝에 대응합니다)

$\setcounter{MaxMatrixCols}{20} \begin{pmatrix} w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 & 0 & 0 & 0 & 0 \\ 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 \\ 0 & 0 & 0 & 0 & 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} \end{pmatrix}$

이 선형 연산은 16차원의 벡테로 변환된 입력을 4차원의 벡터로 만들고 최종적으로 2×2 출력 행렬로 변환됩니다. (역주: [4, 16] 행렬과 [16] 벡터를 행렬곱하면 [4] 벡터가 됩니다)

이런 벡터 표현을 사용하면 역방향 계산(backward pass)은 $C$ 의 전치 행렬을 이용하여 손쉽게 구할 수 있습니다. 다른 말로 하면, 손실(loss)에 $C^T$ 를 곱하여 에러가 역전파되는 것이 한 예입니다. 이 연산은 4차원 벡터를 입력으로 받아 16차원 벡터를 출력으로 만들지만 연결 패턴은 $C$ 를 사용할 때와 동일합니다.

주목할 것은 커널 w가 정방향(forward pass)과 역방향(backward pass) 계산에 사용되는 행렬 $C$ 와 $C^T$ 에 모두 사용됩니다.

4.2 전치(Transposed) 콘볼루션

그림 2.1 에 나타난 콘볼루션의 연결 패턴을 유지하면서 4차원 공간을 16차원 공간에 매핑하는 데 다른 방법이 어떤 것이 있는지 알아보겠습니다. 이 연산을 전치 콘볼루션이라고 부릅니다.

전치 콘볼루션-또는 부분 스트라이드 콘볼루션으로 불리는-은 콘볼루션의 정방향과 역방향을 바꾸어 거꾸로 작동합니다. 다르게 말하면 커널이 콘볼루션을 정의하지만 직접 콘볼루션인지 전치 콘볼루션인지는 어떻게 정방향과 역방향을 계산하느냐로 결정됩니다.

예를 들면 커널 $w$ 가 각각 $C$ 와 $C^T$ 를 곱하여 정방향과 역방향 콘볼루션을 정의했다면 이는 정방향과 역방향에 $C^T$ 와 $(C^T)^T = C$ 를 각각 곱하는 전치 콘볼루션을 정의할 수 있습니다(실제로 전치 콘볼루션을 구현할 때 종종 사용하는 것처럼 전치 콘볼루션의 계산은 입력 값을 콘볼루션의 그래디언트로 생각할 수 있습니다).

(역주: 실제로 텐서플로우는 전치 콘볼루션을 계산할 때 직접 콘볼루션에서 사용하는 역전파 함수에 그래디언트 대신 입력 값을 넣어 사용합니다)

마지막으로 전치 콘볼루션은 직접 콘볼루션(역주: 전치가 아닌 일반 콘볼루션)으로 항상 모사할 수 있습니다. 이 방법의 단점은 입력의 여러 행과 열에 0을 추가해야 해서 불필요한 계산이 늘어납니다.

지금까지 소개한 것을 바탕으로 콘볼루션 계산을 설명한 2장에 역방향 계산을 진행하겠습니다. 같은 커널을 가진 직접 콘볼루션을 참조하면서 전치 콘볼루션의 속성을 유도하겠습니다. 그리고 전치 콘볼루션과 동등한 직접 콘볼루션을 정의합니다.

4.3 제로 패딩 없음, 단일 스트라이드, 전치

전치 콘볼루션을 가장 쉽게 생각하는 방법은 처음에 주어진 입력 크기의 직접 콘볼루션의 출력 크기를 계산하고 전치 콘볼루션을 위해 입력과 출력 크기를 반대로 바꾸는 것입니다.

패딩이 없는 4×4 입력에 단일 스트라이드로 3×3 커널을 콘볼루션하는 예를 생각해 봅시다(즉 $i = 4$ , $k = 3$ , $s = 1$ 그리고 $p = 0$ ). 그림 2.1에서 보듯이 이는 2×2 출력을 만듭니다. 이 콘볼루션의 전치는 2×2 입력이 적용될 때 4×4 크기의 출력을 만들게 됩니다.

전치 콘볼루션의 결과를 얻는 또 다른 방법은 비효율적이지만 동등한 효과를 내는 직접 콘볼루션을 적용하는 것입니다. 그림 4.1에서 2×2 테두리가 제로 패딩된 2×2 입력에 단일 스트라이드로 3×3 커널을 콘볼루션하는 것으로 같은 효과를 내었습니다(즉 $i' = 2$ , $k' = k$ , $s' = 1$ 그리고 $p' = 2$ ). 커널과 스트라이드의 크기는 동일하지만 전치 콘볼루션의 입력은 제로 패딩되었습니다.(이 콘볼루션은 전치 콘볼루션과 동일하지만 추가된 제로 패딩 때문에 그림에서 0을 곱하는 연산이 많이 발생합니다. 하지만 이는 일러스트의 목적을 위해서이며 실제 소프트웨어 구현에서는 0을 곱하는 연산을 수행하지 않습니다.)

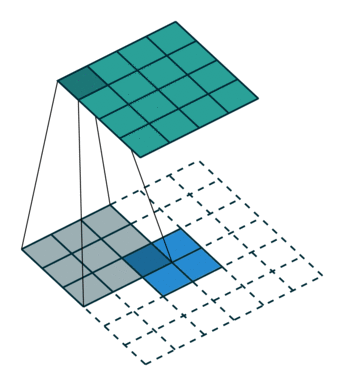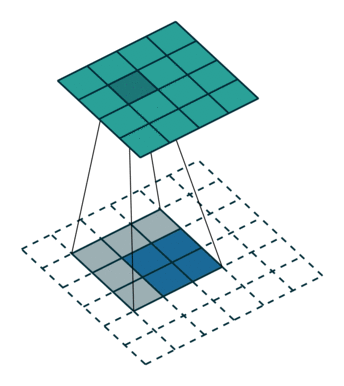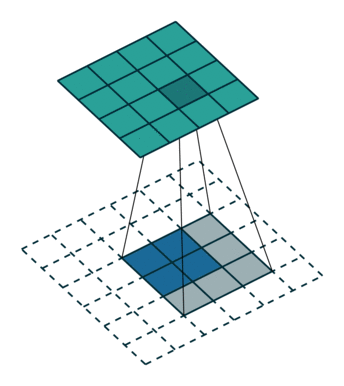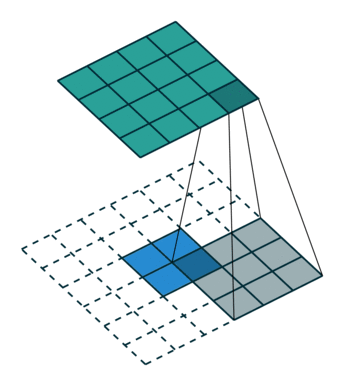
그림 4.1: 4×4 입력에 대해 단일 스트라이드로 3×3 커널을 전치 콘볼루션하기(즉 i = 4, k = 3, s = 1 그리고 p = 0). 이는 2×2 테두리로 제로 패딩된 2×2 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션하는 것과 동일합니다(즉 i’ = 2, k’ = k, s’ = 1 그리고 p’ = 2).

제로 패딩이 되는 원리를 이해하는 한가지 방법은 전치 콘볼루션의 연결 패턴을 고려하여 대등한 콘볼루션을 구성하도록 조정하는 것입니다. 예를 들면, 직접 콘볼루션의 왼쪽 최상단 픽셀은 출력의 왼쪽 최상단 픽셀에만 영향을 끼치고 오른쪽 최상단 픽셀은 출력의 오른쪽 최상단 픽셀과만 연결되는 식입니다.

동일한 연결 패턴을 유지한 대등한 콘볼루션을 만들려면 커널의 첫번째 스텝이 왼쪽 최상단의 픽셀에만 겹쳐지도록 입력에 제로 패딩을 넣는 것이 필요합니다. 결국 패딩은 커널 사이즈보다 하나 작은 크기가 됩니다.

같은 방식으로 진행하면서 이미지의 다른 픽셀에 대해 비슷한 관찰을 수행할 수 있고 다음식이 유도됩니다.

식 8. $s = 1$ , $p = 0$ 그리고 $k$ 인 콘볼루션은 $k' = k$ , $s' = s$ 그리고 $p' = k - 1$ 인 전치 콘볼루션과 연관되어 있습니다. 그리고 출력 크기는,

$o' = i' + (k - 1)$

흥미롭게도 이것은 단일 스트라이드 풀 패딩 콘볼루션과 동일합니다. (역주: 또한 제로 패딩 없는 단일 스트라이드 직접 콘볼루션의 식 1에서 $i$ 와 $o$ 가 바뀐 식입니다)

4.4 제로 패딩, 단일 스트라이드, 전치

제로 패딩이 없는 콘볼루션의 전치가 제로 패딩된 콘볼루션과 동일하다는 것을 알았으므로 제로 패딩이 있는 콘볼루션의 전치는 덜 패딩된 입력을 콘볼루션하는 것과 동일한 것이라고 추측할 수 있습니다.

이는 $i = 5$ , $k = 4$ 그리고 $p = 2$ 인 그림 4.2에 나타난 것처럼 사실입니다. 수식으로 표현하면 아래 식은 제로 패딩된 콘볼루션에 적용됩니다.

식 9. $s = 1$ , $k$ 그리고 $p$ 인 콘볼루션은 $k' = k$ , $s' = s$ 그리고 $p' = k - p - 1$ 인 전치 콘볼루션과 연관되어 있고 이 출력의 크기는,

$o' = i' + (k - 1) - 2p$

(역주: 이는 식 2에서 $i$ 와 $o$ 가 바뀐 식입니다)

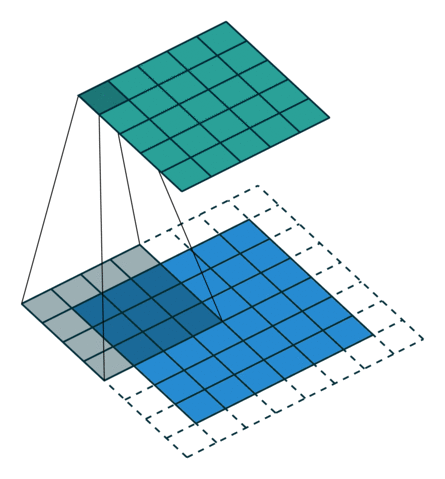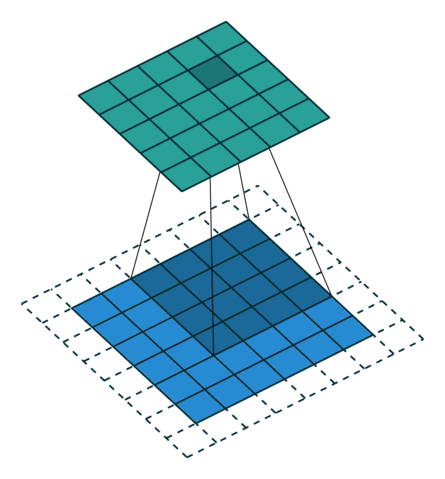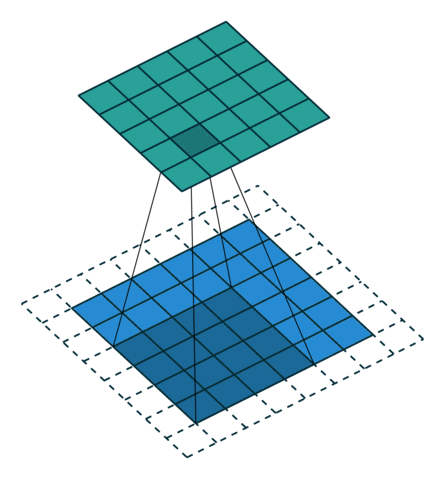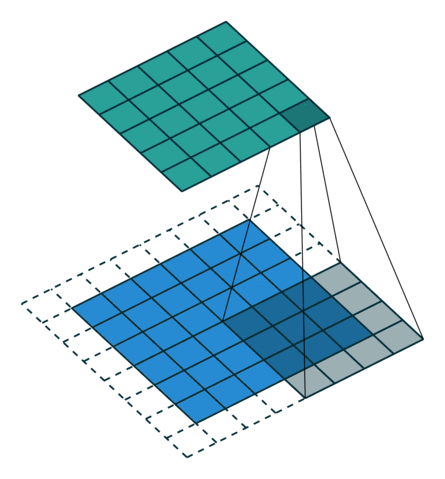
그림 4.2: 2×2 테두리로 제로 패딩된 5×5 입력에 대해 단일 스트라이드로 4×4 커널을 전치 콘볼루션하기(즉 i = 5, k = 4, s = 1 그리고 p = 2). 이는 1×1 테두리로 제로 패딩된 6×6 입력에 대해 단일 스트라이드로 4×4 커널을 콘볼루션하는 것과 동일합니다(즉 i’ = 6, k’ = k, s’ = 1 그리고 p’ = 1).

4.4.1 하프(동일) 패딩, 전치

이전에 했던 것과 같은 논리를 적용하면 출력의 크기가 입력의 크기와 동일한 하프 패딩 콘볼루션의 대등한 전치 콘볼루션은 하프 패딩 콘볼루션 자기 자신이 됩니다. 그러므로 다음 식이 성립됩니다.

식 10. $k = 2n + 1$ , $n \in N$ , $s = 1$ 그리고 $p = \lfloor \dfrac{k}{2} \rfloor = n$ 인 콘볼루션은 $k' = k$ , $s' = s$ 그리고 $p' = p$ 인 전치 콘볼루션과 연관되어 있고 출력 사이즈는,

$o' = i' + (k - 1) - 2p = i' + 2n - 2n = i'$

그림 4.3은 $i = 5$ , $k = 3$ 그리고 $p = 1$ 인 예입니다.

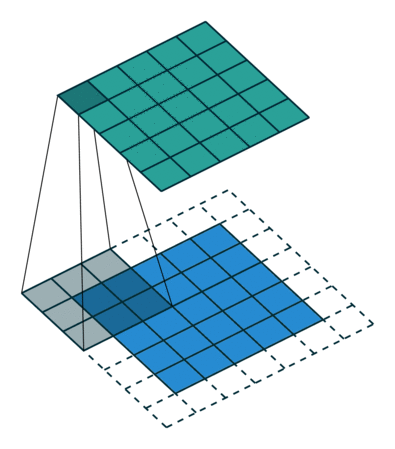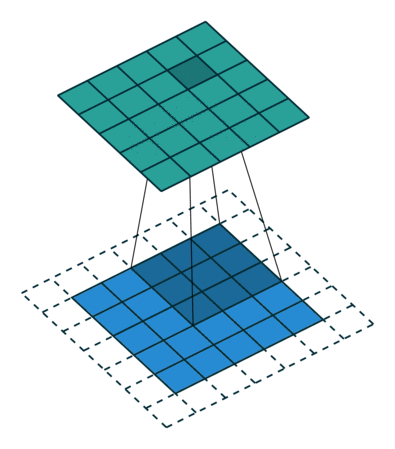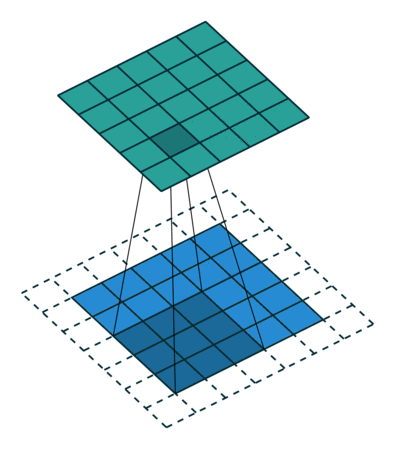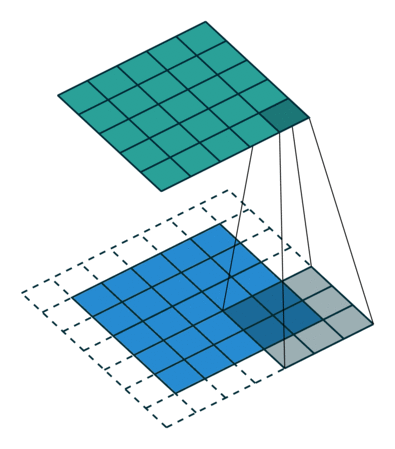
그림 4.3: 하프 패딩된 5×5 입력에 대해 단일 스트라이드로 3×3 커널을 전치 콘볼루션하기(즉 i = 5, k = 3, s = 1 그리고 p = 1). 이는 하프 패딩된 5×5 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션하는 것과 동일합니다(즉 i’ = 5, k’ = k, s’ = 1 그리고 p’ = 1).

4.4.2 풀 패딩, 전치

패딩 없는 콘볼루션의 전치와 대등한 콘볼루션이 풀 패딩이므로 풀 패딩 콘볼루션의 전치와 대등한 것은 패딩 없는 콘볼루션이 되는 것이 자연스럽습니다.

식 11. $s = 1$ , $k$ 그리고 $p = k - 1$ 인 콘볼루션은 $k' = k$ , $s' = s$ 그리고 $p' = 0$ 인 전치 콘볼루션과 연관되어 있고 출력사이즈는,

$o' = i' + (k - 1) - 2p = i - (k - 1)$

(역주: 이는 식 4에서 $i$ 와 $o$ 가 바뀐 식입니다)

그림 4.4는 $i = 5$ , $k = 3$ 그러므로 $p = 2$ 인 예입니다.

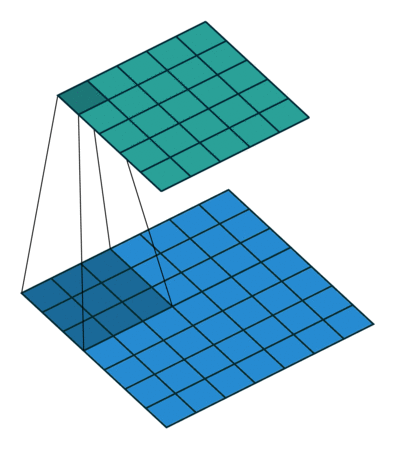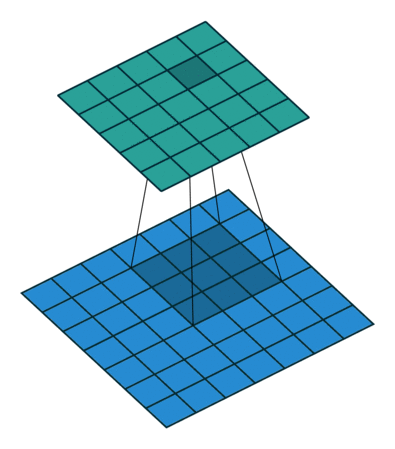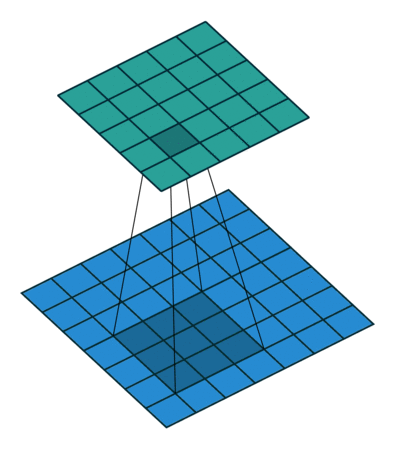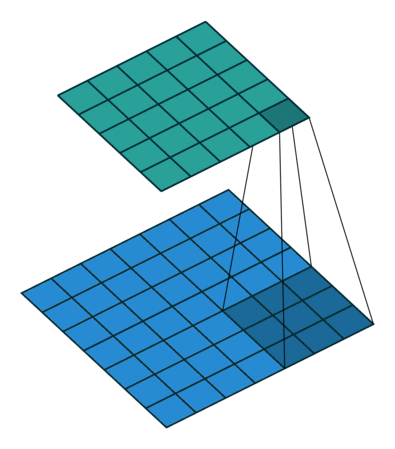
그림 4.4: 풀 패딩된 5×5 입력에 대해 단일 스트라이드로 3×3 커널을 전치 콘볼루션하기(즉 i = 5, k = 3, s = 1 그리고 p = 2). 이는 7×7 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션하는 것과 동일합니다(즉 i’ = 7, k’ = k, s’ = 1 그리고 p’ = 0).

4.5 제로 패딩 없음, 다중 스트라이드, 전치

제로 패딩 콘볼루션에 적용했던 원리를 동일하게 사용하면 $s > 1$ 인 콘볼루션의 전치는 $s < 1$ 인 동등한 콘볼루션과 관련이 있다고 기대할 수 있습니다. 앞으로 설명하겠지만 이 직감은 맞습니다. 그래서 전치 콘볼루션을 부분 스트라이드 콘볼루션으로 부르기도 합니다.

그림 4.5는 $i = 5$ , $k = 3$ 그리고 $s = 2$ 인 예로서 부분 스트라이드가 무엇인지 잘 보여줍니다. 즉 0이 입력 원소 사이에 추가되어서 커널이 단일 스트라이드일 때 보다 더 느리게 움직이게 만듭니다.(이렇게 하는 것은 비효율적이라 실제 구현에서는 불필요하게 0을 곱하는 것을 피합니다. 여기서는 개념적으로 스트라이드 콘볼루션의 전치를 보여주기 위해서 입니다.)

여기서는 이 콘볼루션이 패딩이 없는( $p = 0$ ) 콘볼루션이고 $i - k$ 가 $s$ 의 배수인 $i$ 가 입력의 크기라고 가정합니다. 이 경우 다음식이 성립됩니다.(역주: 식 5에서 내림[floor] 함수를 떼어내기 위한 가정입니다)

식 12. $p = 0$ , $k$ , $s$ 그리고 $i -k$ 가 $s$ 의 배수인 입력 크기( $i$ )를 가진 콘볼루션은 $\tilde{i}'$ , $k' = k$ , $s' = 1$ 그리고 $p' = k - 1$ 인 전치 콘볼루션과 연관되어 있습니다. 여기서 $\tilde{i}'$ 는 입력의 원소 사이사이에 $s - 1$ 의 0이 추가되어 늘어난 크기 입니다. 이 출력의 크기는,

$o' = s(\tilde{i}' - 1) + k$

(역주: 이는 식 5에서 내림 함수를 떼고 난 후 $i$ 와 $o$ 가 바뀐 식입니다)

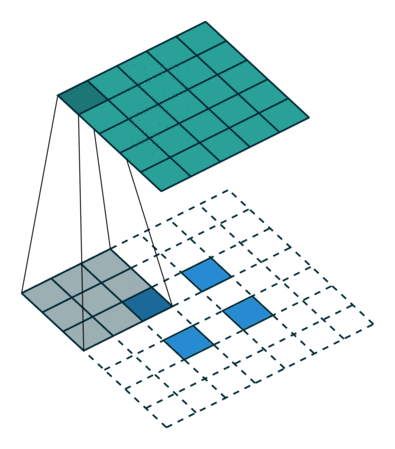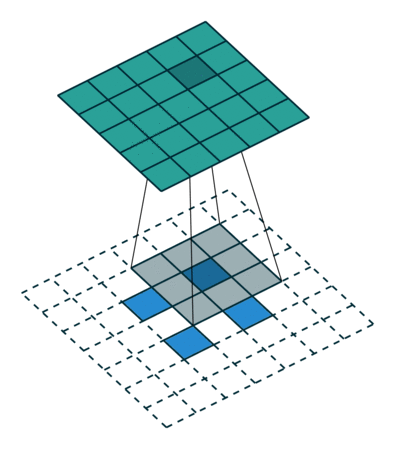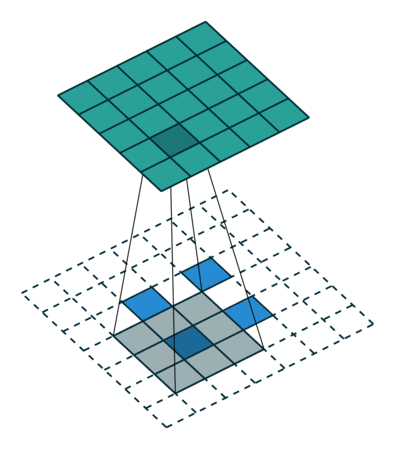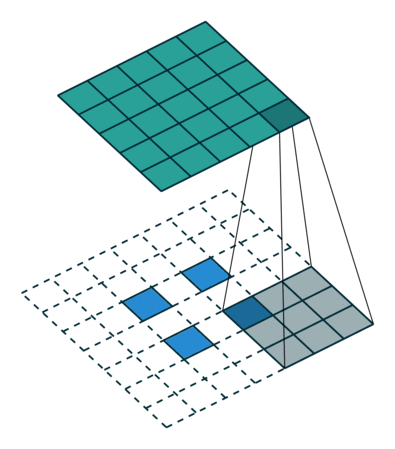
그림 4.5: 5×5 입력에 대해 2×2 스트라이드로 3×3 커널을 전치 콘볼루션하기(즉 i = 5, k = 3, s = 2 그리고 p = 0). 이는 2×2 테두리로 제로 패딩되고 입력 원소 사이에 1개의 0이 추가된 2×2 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션하는 것과 동일합니다(즉 i’ = 2, $\tilde{i}'$ = 3, k’ = k, s’ = 1 그리고 p’ = 2)

4.6 제로 패딩, 다중 스트라이드, 전치

콘볼루션의 입력이 $i + 2p - k$ 가 $s$ 의 배수인 $i$ 의 크기를 가질 때 식 9와 식 12를 조합하여 제로 패딩된 경우로 확장시킬 수 있습니다.(역주: 식 6에서 내림[floor] 함수를 떼어내기 위한 가정입니다)

식 13. $k$ , $s$ , $p$ 그리고 $i + 2p - k$ 가 $s$ 의 배수인 $i$ 를 가지는 콘볼루션은 $\tilde{i}'$ , $k' = k$ , $s' = 1$ 그리고 $p' = k - p - 1$ 인 전치 콘볼루션과 관련이 있습니다. 여기서 $\tilde{i}'$ 는 입력의 각 원소 사이에 $s - 1$ 개의 0이 추가되어 늘어난 입력 크기 입니다. 이 출력의 크기는,

$o' = s(\tilde{i}' - 1) + k - 2p$

(역주: 이는 식 6에서 내림 함수를 떼고 난 후 $i$ 와 $o$ 가 바뀐 식입니다)

그림 4.6은 $i = 5$ , $k = 3$ , $s = 2$ 그리고 $p = 1$ 인 예입니다.

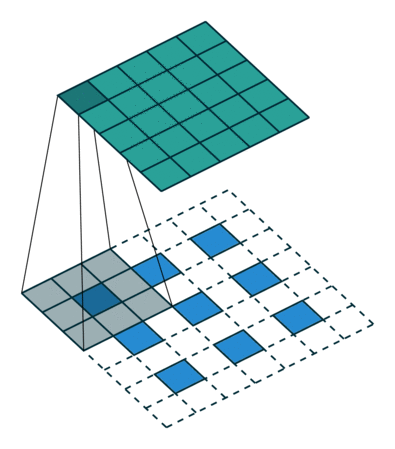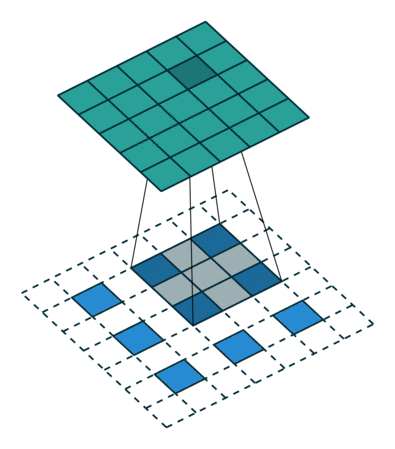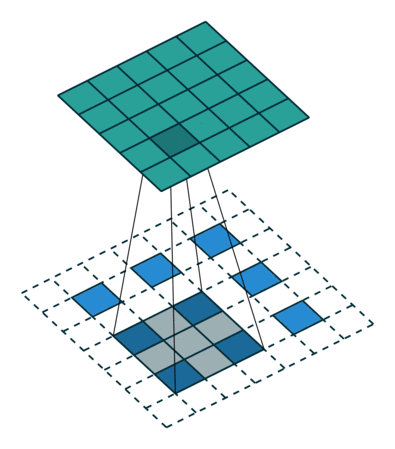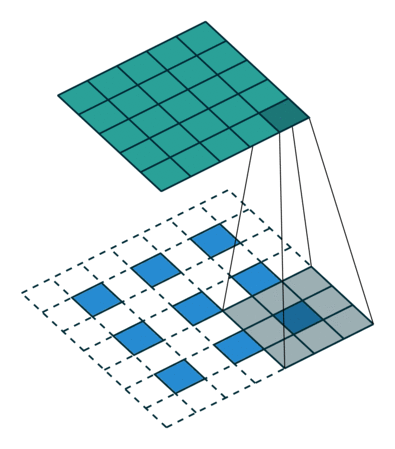
그림 4.6: 1×1 테두리로 제로 패딩된 5×5 입력에 대해 2×2 스트라이드로 3×3 커널을 전치 콘볼루션하기(즉 i = 5, k = 3, s = 2 그리고 p = 1). 이는 1×1 테두리로 제로 패딩되고 입력 원소 사이에 1개의 0이 삽입된 3×3 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션하는 것과 동일합니다(즉 i’=3, $\tilde{i}'$ = 5, k’ = k, s’ = 1 그리고 p’ = 1).

$s$ 가 동일할 때 같은 $i'$ 를 만드는 입력 사이즈 $i$ 를 추가적인 파라메타 $a \in {0, ... , s-1}$ 로 표현을 확장할 수 있습니다.

식 14. $k$ , $s$ , $p$ 인 콘볼루션은 $\tilde{i}'$ , $k' = k$ , $s' = 1$ 그리고 $p' = k - p - 1$ 인 전치 콘볼루션과 관련이 있습니다. 여기서 $\tilde{i}'$ 는 입력의 각 원소 사이에 s – 1 개의 0이 추가되어 늘어난 입력의 크기 이고 $a = (i + 2p - k) mod s$ 는 입력의 상단과 오른쪽에 추가된 0의 갯수를 나타냅니다. 이 출력의 크기는,

$o' = s(\tilde{i}' - 1) + a + k - 2p$

(역주: 이는 식 6에서 내림 함수를 고려하여 $i$ 와 $o$ 를 바꾼 식입니다)

그림 4.7은 $i = 6$ , $k = 3$ , $s = 2$ 그리고 $p = 1$ 인 예입니다.

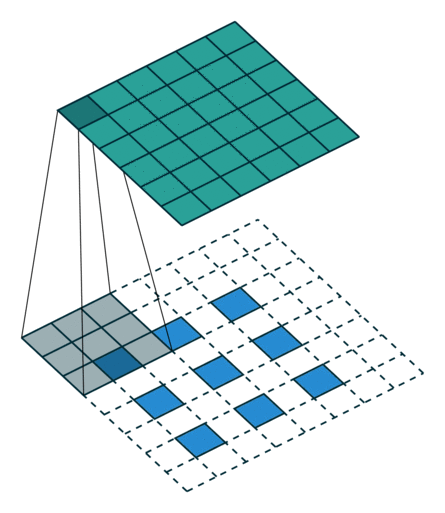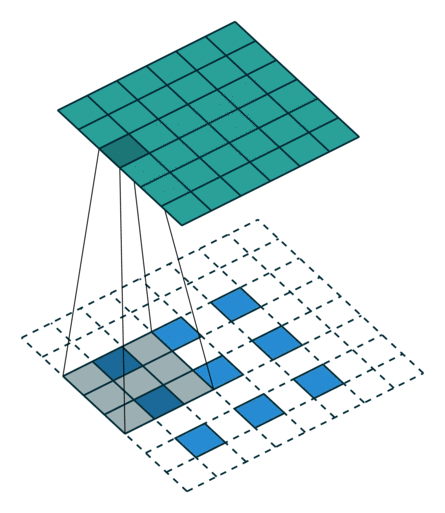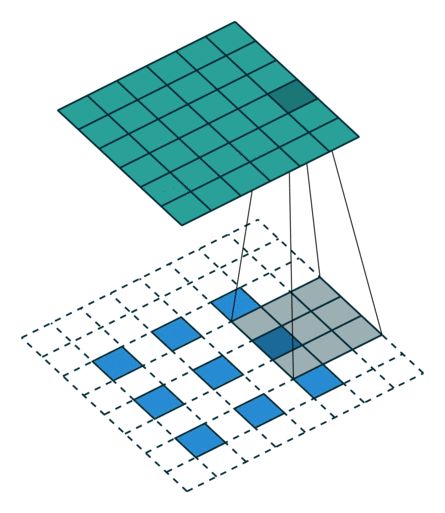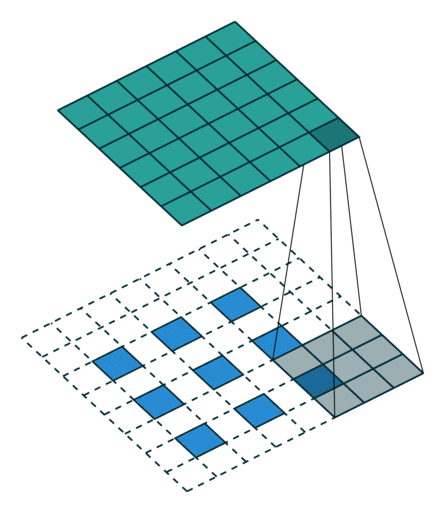
그림 4.7: 1×1 테두리로 제로 패딩된 6×6 입력에 대해 2×2 스트라이드로 3×3 커널을 전치 콘볼루션하기(즉 i = 6, k = 3, s = 2 그리고 p = 1). 이는 1×1 테두리와 위와 오른쪽에 하나가 추가로 제로 패딩되고 입력의 원소 사이에 1개의 0이 삽입된 3×3 입력에 대해 단일 스트라이드로 3×3 커널을 콘볼루션하는 것과 동일합니다(즉 i’ = 3, $\tilde{i}'$ = 5, a = 1, k’ = k, s’ = 1 그리고 p’ = 1).

참고 문헌

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G. S., Davis, A., Dean, J., Devin, M., et al. (2015). Tensorflow: Large-scale machine learning on heterogeneous systems. Software available from tensorflow.org .
Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I., Bergeron, A., Bouchard, N., Warde-Farley, D., and Bengio, Y. (2012). Theano: new features and speed improvements. arXiv preprint arXiv:1211.5590.
Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., Turian, J., Warde-Farley, D., and Bengio, Y. (2010). Theano: A cpu and gpu math compiler in python. In Proc. 9th Python in Science Conf , pages 1–7.
Boureau, Y., Bach, F., LeCun, Y., and Ponce, J. (2010a). Learning mid-level features for recognition. In Proc. International Conference on Computer Vision and Pattern Recognition (CVPR’10). IEEE.
Boureau, Y., Ponce, J., and LeCun, Y. (2010b). A theoretical analysis of feature pooling in vision algorithms. In Proc. International Conference on Machine learning (ICML’10).
Boureau, Y., Le Roux, N., Bach, F., Ponce, J., and LeCun, Y. (2011). Ask the locals: multi-way local pooling for image recognition. In Proc. International Conference on Computer Vision (ICCV’11). IEEE.
Collobert, R., Kavukcuoglu, K., and Farabet, C. (2011). Torch7: A matlab-like environment for machine learning. In BigLearn, NIPS Workshop, number EPFL-CONF-192376.
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep learning. Book in preparation for MIT Press.
Im, D. J., Kim, C. D., Jiang, H., and Memisevic, R. (2016). Generating images with recurrent adversarial networks. arXiv preprint arXiv:1602.05110.
Jia, Y., Shelhamer, E., Donahue, J., Karayev, S., Long, J., Girshick, R., Guadar-rama, S., and Darrell, T. (2014). Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the ACM International Conference on Multimedia, pages 675–678. ACM.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105.
Le Cun, Y., Bottou, L., and Bengio, Y. (1997). Reading checks with multilayer graph transformer networks. In Acoustics, Speech, and Signal Processing, 1997. ICASSP-97., 1997 IEEE International Conference on, volume 1, pages 151–154. IEEE.
Long, J., Shelhamer, E., and Darrell, T. (2015). Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 3431–3440.
Radford, A., Metz, L., and Chintala, S. (2015). Unsupervised representa- tion learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434.
Saxe, A., Koh, P. W., Chen, Z., Bhand, M., Suresh, B., and Ng, A. (2011). On random weights and unsupervised feature learning. In L. Getoor and T. Scheffer, editors, Proceedings of the 28th International Conference on Machine Learning (ICML-11), ICML ’11, pages 1089–1096, New York, NY, USA. ACM.
Visin, F., Kastner, K., Courville, A. C., Bengio, Y., Matteucci, M., and Cho, K. (2015). Reseg: A recurrent neural network for object segmentation.
Zeiler, M. D. and Fergus, R. (2014). Visualizing and understanding convolu-tional networks. In Computer vision–ECCV 2014, pages 818–833. Springer.
Zeiler, M. D., Taylor, G. W., and Fergus, R. (2011). Adaptive deconvolutional networks for mid and high level feature learning. In Computer Vision (ICCV), 2011 IEEE International Conference on, pages 2018–2025. IEEE.

	박해선 (“실무로 통하는 ML 문제 해결 with 파…)
	sharp2h2 (“실무로 통하는 ML 문제 해결 with 파…)
	박해선 (“실무로 통하는 ML 문제 해결 with 파…)
	효효효 (“실무로 통하는 ML 문제 해결 with 파…)
	박해선 (Machine Learning with Python C…)
	코린이 (Machine Learning with Python C…)
	박해선 (“머신 러닝 교과서: 파이토치 편…)
	책구매자 (“머신 러닝 교과서: 파이토치 편…)
	박해선 (Machine Learning with Python C…)
	ddddd (Machine Learning with Python C…)
	박해선 (Essential Math for Data Scienc…)
	dk kkk (Essential Math for Data Scienc…)
	이시은 (About Me)
	박해선 (About Me)
	이시은 (About Me)

텐서 플로우 블로그 (Tensor ≈ Blog)

머신러닝(Machine Learning), 딥러닝(Deep Learning) 그리고 텐서(Tensor) 또 파이썬(Python)

A guide to convolution arithmetic for deep learning

딥 러닝을 위한 콘볼루션 계산 가이드

감사의 말

피드백

소스코드와 이미지

목차

1장. 소개

1.1 분할 콘볼루션(Discrete convolutions)

1.2 풀링(Pooling)

2장. 콘볼루션 계산

2.1 제로 패딩 없음, 단일 스트라이드

2.2 제로 패딩, 단일 스트라이드

2.2.1 하프(half, 또는 동일) 패딩

2.2.2 풀(full) 패딩

2.3 제로 패딩 없음, 다중 스트라이드

2.4 제로 패딩, 다중 스트라이드

3장. 풀링(Pooling) 계산

4장. 전치(transposed) 콘볼루션 계산

4.1 행렬 연산으로 표현한 콘볼루션

4.2 전치(Transposed) 콘볼루션

4.3 제로 패딩 없음, 단일 스트라이드, 전치

4.4 제로 패딩, 단일 스트라이드, 전치

4.4.1 하프(동일) 패딩, 전치

4.4.2 풀 패딩, 전치

4.5 제로 패딩 없음, 다중 스트라이드, 전치

4.6 제로 패딩, 다중 스트라이드, 전치

참고 문헌

댓글 남기기 응답 취소

딥 러닝을 위한 콘볼루션 계산 가이드

감사의 말

피드백

소스코드와 이미지

목차

1장. 소개

1.1 분할 콘볼루션(Discrete convolutions)

1.2 풀링(Pooling)

2장. 콘볼루션 계산

2.1 제로 패딩 없음, 단일 스트라이드

2.2 제로 패딩, 단일 스트라이드

2.2.1 하프(half, 또는 동일) 패딩

2.2.2 풀(full) 패딩

2.3 제로 패딩 없음, 다중 스트라이드

2.4 제로 패딩, 다중 스트라이드

3장. 풀링(Pooling) 계산

4장. 전치(transposed) 콘볼루션 계산

4.1 행렬 연산으로 표현한 콘볼루션

4.2 전치(Transposed) 콘볼루션

4.3 제로 패딩 없음, 단일 스트라이드, 전치

4.4 제로 패딩, 단일 스트라이드, 전치

4.4.1 하프(동일) 패딩, 전치

4.4.2 풀 패딩, 전치

4.5 제로 패딩 없음, 다중 스트라이드, 전치

4.6 제로 패딩, 다중 스트라이드, 전치

참고 문헌

이 글 공유하기:

댓글 남기기 응답 취소