경사하강법^{gradient descent} 최적화 알고리즘의 한 종류인 모멘텀^momentum과 네스테로프 모멘텀^{nesterov momentum} 방식은 여러 신경망 모델에서 널리 사용되고 있습니다. 비교적 이 두가지 알고리즘은 직관적이고 쉽게 이해할 수 있습니다. 이 글에서는 두 알고리즘이 실제 구현에서는 어떻게 적용되는지 살펴 보겠습니다.

모멘텀 알고리즘은 누적된 과거 그래디언트가 지향하고 있는 어떤 방향을 현재 그래디언트에 보정하려는 방식입니다. 일종의 관성 또는 가속도처럼 생각하면 편리합니다. 머신 러닝의 다른 알고리즘들이 그렇듯이 모멘텀 공식도 쓰는 이마다 표기법이 모두 다릅니다. 여기에서는 일리아 서스키버^{Ilya Sutskever}의 페이퍼¹에 있는 표기를 따르겠습니다. 모멘텀 알고리즘의 공식은 아래와 같습니다.

은 학습속도이고 는 모멘트 효과에 대한 가중치입니다. 는 0 으로 초기화되어 있고 반복이 될 때마다 현재의 그래디언트  가 다음번 모멘트 에 누적됩니다. 그리고 다음번 반복에서 가 현재의 모멘트  로 사용됩니다. 경사하강법에서 모멘트 항이 추가된 것입니다.

이 그림은 일리아 서스키버의 페이퍼¹에서 캡쳐한 것입니다. 윗쪽의 그림이 일반 모멘텀 방식을 설명해 주고 있습니다. 파라미터 공간의 현재 위치 이전까지 누적된 그래디언트 벡터가 입니다. 현재 위치의 그래디언트과 구분하기 위해 편의상 이 누적된 그래디언트를 속도라고 부르겠습니다. 속도는 그대로 사용하는 것이 아니고 공식에 표현되어 있듯이 적절한 를 곱합니다. 현재 위치에서의 그래디언트와 속도를 더해 구해진 가  에 더해지면   가 됩니다. 이런 모멘텀은 그래디언트가 큰 흐름의 방향을 지속하도록 도와 줍니다. 아래 그림은 이런 모멘트의 효과를 그림으로 표현하고 있습니다.²

그럼 네스테로프 모멘텀은 어떻게 다를까요. Figure 1 의 하단 그림과 아래 공식을 함께 보면 조금 더 이해가 쉽습니다.

이 공식은 모멘텀의 공식과 거의 같습니다. 다만 현재 위치의 그래디언트 를 이용하는 것이 아니고 현재 위치에서 속도 만큼 전진한 후의 그래디언트  를 이용합니다. 사람들은 이를 가리켜 선험적으로 혹은 모험적으로 먼저 진행한 후 에러를 교정한다라고 표현합니다. 궁금한 점은 현재 파라미터 위치에서 앞쪽의 그래디언트를 구한다는 것입니다. 반복 루프 안에서 학습이 진행되는 경사하강법의 알고리즘에서 앞선 그래디언트를 어떻게 구하는 것일까요.

모멘텀 방식과 네스테로프 모멘텀은 확실히 다릅니다. 아래 그림에서 편의상 동일 지점에서 모멘텀과 네스테로프 모멘텀을 한번에 나타내었습니다. 이 그림에서 볼 수 있듯이 만큼 이동한 후 현재의 그래디언트 로 진행하는 것과 만큼 이동한 지점의 그래디언트 로 진행하는 것은 다른 결과를 가져다 줍니다.

네스테로프 모멘텀의 진행과정을 조금 더 자세히 보기 위해 반복 스텝 t 의 전후를 이어서 그려 보겠습니다.

우리가 위에서 본 네스테로프 모멘텀 공식으로 현재 에서 로 이동하기 위한 를 구하면  입니다. 그리고 는 다음번 반복에서 가 되어 새로운 모멘텀 항에 사용됩니다. 앞서 이야기한 것 처럼 에서 그래디언트를 구하기 위해 코드를 구성하려면 왠지 코드가 복잡해 질 것 같습니다. 그래서 네스테로프를 구현한 여러 코드에서는 약간의 트릭을 사용합니다. 위 그림에서 의 위치를 한걸음 뒤로 물려 보겠습니다.

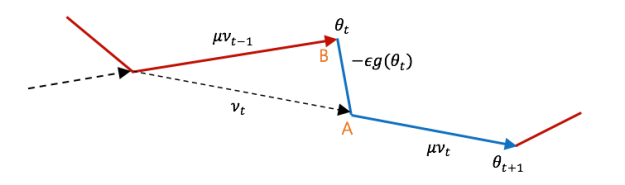
위 그림에서 와 에 집중하기 위해 다른 표시들은 삭제했습니다. 가 A 지점에서 B 지점으로 옮겨졌습니다. 이에 따라 가 간단하게 로 바뀌었습니다. 를 옮기기 전과 후의 값은 확실히 다릅니다. 하지만 네스테로프 모멘텀의 경로를 그대로 따르고 있으므로 학습을 많이 반복하여 최적점에 수렴하면 전체 파라미터 공간에서 A 지점과 B 지점은 거의 동일하게 될 것입니다.

현재 위치에서 는 얻을 수 있고 필요한 것은 입니다. 위 그림에서 볼 수 있듯이 입니다. 따라서 아래와 같이 쓸 수 있습니다.

에서 만큼 이동하고 다음에 를 진행하는 전체 식을 다시 살펴 보면 다음과 같습니다.

이렇게 쓰면 현재 그래디언트와 이전의 속도만 가지고 네스테로프 모멘텀의 궤적을 따라갈 수 있습니다. 사실 이 식은 요수아 벤지오^{Yoshua Bengio} 교수의 페이퍼³에 잘 설명되어 있습니다. 다만 식을 쓰는 순서가 조금 다를 뿐입니다. 안드레이 카패시^{Andrej Karpathy}도 CS231n 강의 노트⁴에 벤지오 교수의 표기와 유사하게 설명하고 있습니다. 위 그림을 CS231n 강의 노트 표기로 바꾸어 나타내어 보면 아래와 같습니다.

v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form

이제 조금더 명확해 진 것 같습니다. 하지만 실제 코드들은 벤지오 교수의 표기 보다는 아래와 같이 쓰는 것을 즐겨합니다.

또 이식은 다음처럼 나누어 쓰면 패턴이 잘 보입니다.

이렇게 보면 가 보통 모멘텀과 완전히 동일하고 이 값을 한번 더 모멘텀 공식에 넣고 있습니다. 의 어느 지점에서 네스테로프 모멘텀은 일반 모멘텀으로 구한 속도를 이전 속도라고 가정하고 다시 모멘텀 방식을 적용한 것입니다. 조금 복잡하지만 굳이 그림으로 나타내 보면 아래와 같습니다.

여기에서 는 에서의 일반 모멘텀이고 은 네스테로프 모멘텀입니다. 이 그림은 어느 지점에서 모멘텀과 네스테로프 모멘텀을 가상으로 표현한 것이고 실제 두 알고리즘이 만드는 전체 궤적은 다릅니다.

그럼 실제 코드 구현을 확인해 보겠습니다. 제가 눈으로 확인한 것은 사이킷런^scikit-learn의 멀티레이어 퍼셉트론^{multi-layer perceptron}의 구현⁵과 케라스^Keras의 구현⁶입니다.

사이킷런의 SGDOptimizer 클래스 중 일부 코드입니다.

updates = [self.momentum * velocity - self.learning_rate * grad
           for velocity, grad in zip(self.velocities, grads)]
self.velocities = updates

if self.nesterov:
    updates = [self.momentum * velocity - self.learning_rate * grad
               for velocity, grad in zip(self.velocities, grads)]

다음은 케라스의 SGD 클래스 중 일부 코드입니다.

v = self.momentum * m - lr * g # velocity
self.updates.append(K.update(m, v))

if self.nesterov:
    new_p = p + self.momentum * v - lr * g
else:
    new_p = p + v

코드를 보면 이해가 더 잘 됩니다. 이렇게 네스테로프 모멘텀을 일반 모멘텀을 이용해 구하는 방식은 코드를 깔끔하고 읽기 좋게 만들어 줍니다. 사실 되짚어 보면 이런 테크닉이 매우 난해한 것은 아닙니다. 다만 구현된 코드들에 별다른 설명이 없고 대부분의 네스테로프 모멘텀의 방정식이 일리아 서스키버의 표현 방식으로 기술되어 있어서 처음 볼 때 고개를 갸우뚱하게 되는 것 같습니다. 🙂

---

1. Ilya Sutskever, James Martens, George Dahl, Geoffrey Hinton. 2013. On the importance of initialization and momentum in deep. pdf
2. Sebastian Ruder. 2016. An overview of gradient descent optimization algorithms. 1609.04747
3. Yoshua Bengio, Nicolas Boulanger-Lewandowski, Razvan Pascanu. 2012. Advances in Optimizing Recurrent Networks. 1212.0901
4. CS231n Convolutional Neural Networks for Visual Recognition. website.
5. https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/neural_network/_stochastic_optimizers.py
6. https://github.com/fchollet/keras/blob/master/keras/optimizers.py