2.3.4 나이브 베이즈 분류기 | 목차 | 2.3.6 결정 트리의 앙상블
–
결정 트리decision tree는 분류와 회귀 문제에 널리 사용하는 모델입니다. 기본적으로 결정 트리는 결정에 다다르기 위해 예/아니오 질문을 이어 나가면서 학습합니다.
이 질문은 스무고개 놀이의 질문과 비슷합니다. 곰, 매, 펭귄, 돌고래라는 네 가지 동물을 구분한다고 생각해봅시다. 우리의 목표는 가능한 한 적은 예/아니오 질문으로 문제를 해결하는 것입니다. 날개가 있는 동물인지를 물어보면 가능성 있는 동물을 둘로 좁힐 수 있습니다. 대답이 “yes”이면 다음엔 독수리와 펭귄을 구분할 수 있는 질문을 해야 합니다. 예를 들면 날 수 있는 동물인지 물어봐야 합니다. 만약 날개가 없다면 가능한 동물은 곰과 돌고래가 될 것입니다. 이제 이 두 동물을 구분하기 위한 질문을 해야 합니다. 예를 들면 지느러미가 있는지를 물어봐야 합니다.
연속된 질문들을 [그림 2-22]처럼 결정 트리로 나타낼 수 있습니다.
In[57]:
mglearn.plots.plot_animal_tree()

그림 2-22 몇 가지 동물들을 구분하기 위한 결정 트리
이 그림에서 트리의 노드는 질문이나 정답을 담은 네모 상자입니다(특히 마지막 노드는 리프leaf라고도 합니다). 엣지edge는 질문의 답과 다음 질문을 연결합니다.
머신러닝 식으로 말하면 세 개의 특성 “날개가 있나요?”, “날 수 있나요?”, “지느러미가 있나요?”를 사용해 네 개의 클래스(매, 펭귄, 돌고래, 곰)를 구분하는 모델을 만든 것입니다. 이런 모델을 직접 만드는 대신 지도 학습 방식으로 데이터로부터 학습할 수 있습니다.
결정 트리 만들기
[그림 2-23]의 2차원 데이터셋을 분류하는 결정 트리를 만들어보겠습니다. 이 데이터셋은 각 클래스에 데이터 포인트가 50개씩 있고 반달 두 개가 포개진 듯한 모양을 하고 있습니다. 이 데이터셋을 two_moons라고 하겠습니다.
결정 트리를 학습한다는 것은 정답에 가장 빨리 도달하는 예/아니오 질문 목록을 학습한다는 뜻입니다. 머신러닝에서는 이런 질문들을 테스트라고 합니다(모델이 잘 일반화되었는지를 테스트할 때 사용하는 데이터, 즉 테스트 세트와 혼동하지 마세요). 보통 데이터는 앞서의 동물 구분 예제에서처럼 예/아니오 형태의 특성으로 구성되지 않고, [그림 2-23]의 2차원 데이터셋과 같이 연속된 특성으로 구성됩니다. 연속적인 데이터에 적용할 테스트는 “특성 i는 값 a보다 큰가?”와 같은 형태를 띱니다.
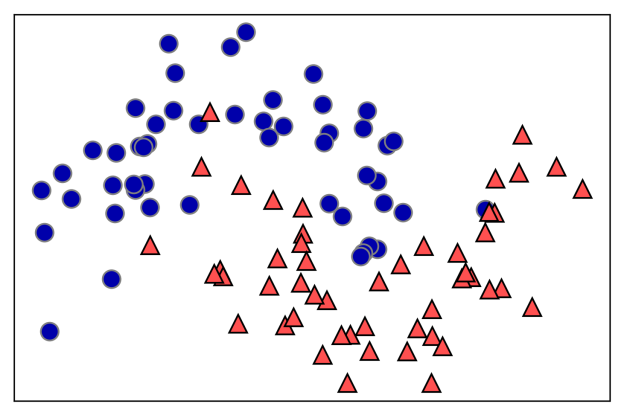
그림 2-23 결정 트리를 적용할 반달 모양의 데이터셋
트리를 만들 때 알고리즘은 가능한 모든 테스트에서 타깃값에 대해 가장 많은 정보를 가진 것을 고릅니다. [그림 2-24]는 첫 번째로 선택된 테스트를 보여줍니다. 데이터셋을 x[1]=0.0596에서 수평으로 나누는 것이 가장 많은 정보를 포함합니다. 즉 이 직선이 클래스 0에 속한 포인트와 클래스 1에 속한 포인트를 가장 잘 나누고 있습니다. 1 루트 노드root node라 불리는 맨 위 노드는 클래스 0에 속한 포인트 50개와 클래스 1에 속한 포인트 50개를 모두 포함한 전체 데이터셋을 나타냅니다. 직선이 의미하는 x[1]<=0.0596의 테스트에서 분기가 일어납니다. 이 테스트를 통과하면 포인트는 왼쪽 노드에 할당되는데 이 노드에는 클래스 0에 속한 포인트는 2개, 클래스 1에 속한 포인트는 32개입니다. 그렇지 않으면 포인트는 오른쪽 노드에 할당되며 이 노드에는 클래스 0의 포인트 48개, 클래스 1의 포인트 18개가 포함되었습니다. 이 두 노드는 [그림 2-24]의 윗부분과 아랫부분에 해당합니다. 첫 번째 분류가 두 클래스를 완벽하게 분류하지 못해서 아래 영역에는 아직 클래스 0에 속한 포인트가 들어 있고 위 영역에는 클래스 1에 속한 포인트가 포함되어 있습니다. 이 두 영역에서 가장 좋은 테스트를 찾는 과정을 반복해서 모델을 더 정확하게 만들 수 있습니다. [그림 2-25]는 가장 많은 정보를 담을 수 있도록 x[0] 값을 기준으로 왼쪽과 오른쪽 영역으로 나누고 있습니다.

그림 2-24 깊이 1인 결정 트리(오른쪽)가 만든 결정 경계(왼쪽)
그림 2-25 깊이 2인 결정 트리(오른쪽)가 만든 결정 경계(왼쪽)
반복된 프로세스는 각 노드가 테스트 하나씩을 가진 이진 결정 트리를 만듭니다. 다르게 말하면 각 테스트는 하나의 축을 따라 데이터를 둘로 나누는 것으로 생각할 수 있습니다. 이는 계층적으로 영역을 분할해가는 알고리즘이라고 할 수 있습니다. 각 테스트는 하나의 특성에 대해서만 이루어지므로 나누어진 영역은 항상 축에 평행합니다.
데이터를 분할하는 것은 각 분할된 영역이 (결정 트리의 리프) 한 개의 타깃값(하나의 클래스나 하나의 회귀 분석 결과)을 가질 때까지 반복됩니다. 타깃 하나로만 이뤄진 리프 노드를 순수 노드pure node라고 합니다. 이 데이터셋에 대한 최종 분할 트리는 [그림 2-26]과 같습니다.
그림 2-26 깊이 9인 결정 트리의 일부(오른쪽)와 이 트리가 만든 결정 경계(왼쪽)(전체 트리는 너무 커서 일부만 표시했습니다.) 2
새로운 데이터 포인트에 대한 예측은 주어진 데이터 포인트가 특성을 분할한 영역들 중 어디에 놓이는지를 확인하면 됩니다. 그래서 그 영역의 타깃값 중 다수(순수 노드라면 하나)인 것을 예측 결과로 합니다. 루트 노드에서 시작해 테스트의 결과에 따라 왼쪽 또는 오른쪽으로 트리를 탐색해나가는 식으로 영역을 찾을 수 있습니다.
같은 방법으로 회귀 문제에도 트리를 사용할 수 있습니다. 예측을 하려면 각 노드의 테스트 결과에 따라 트리를 탐색해나가고 새로운 데이터 포인트에 해당되는 리프 노드를 찾습니다. 찾은 리프 노드의 훈련 데이터 평균 값이 이 데이터 포인트의 출력이 됩니다.
결정 트리의 복잡도 제어하기
일반적으로 트리 만들기를 모든 리프 노드가 순수 노드가 될 때까지 진행하면 모델이 매우 복잡해지고 훈련 데이터에 과대적합됩니다. 순수 노드로 이루어진 트리는 훈련 세트에 100% 정확하게 맞는다는 의미입니다. 즉 훈련 세트의 모든 데이터 포인트는 정확한 클래스의 리프 노드에 있습니다. [그림 2-26]의 왼쪽 그래프가 과대적합된 것으로 볼 수 있습니다. 클래스 0으로 결정된 영역이 클래스 1에 속한 포인트들로 둘러쌓인 것을 볼 수 있습니다. 그 반대 모습도 보입니다. 이는 바람직한 결정 경계의 모습이 아닙니다. 결정 경계가 클래스의 포인트들에서 멀리 떨어진 이상치outlier 하나에 너무 민감하기 때문입니다.
과대적합을 막는 전략은 크게 두 가지입니다. 트리 생성을 일찍 중단하는 전략(사전 가지치기pre-pruning)과 트리를 만든 후 데이터 포인트가 적은 노드를 삭제하거나 병합하는 전략입니다(사후 가지치기post-pruning 또는 그냥 가지치기pruning). 사전 가지치기 방법은 트리의 최대 깊이나 리프의 최대 개수를 제한하거나, 또는 노드가 분할하기 위한 포인트의 최소 개수를 지정하는 것입니다.
scikit-learn에서 결정 트리는 DecisionTreeRegressor와 DecisionTreeClassifier에 구현되어 있습니다. scikit-learn은 사전 가지치기만 지원합니다.
유방암 데이터셋을 이용하여 사전 가지치기의 효과를 자세히 확인해보겠습니다. 항상 그랬듯이 먼저 데이터셋을 읽은 후 훈련 세트와 테스트 세트로 나눕니다. 그런 후에 기본값 설정으로 완전한 트리(모든 리프 노드가 순수 노드가 될 때까지 생성한 트리) 모델을 만듭니다. random_state 옵션을 고정해 만들어진 트리를 같은 조건으로 비교합니다.
In[59]:
from sklearn.tree import DecisionTreeClassifier
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(tree.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(tree.score(X_test, y_test)))
Out[59]:
훈련 세트 정확도: 1.000 테스트 세트 정확도: 0.937
기대한 대로 모든 리프 노드가 순수 노드이므로 훈련 세트의 정확도는 100%입니다. 즉 트리는 훈련 데이터의 모든 레이블을 완벽하게 기억할 만큼 충분히 깊게 만들어졌습니다. 테스트 세트의 정확도는 이전에 본 선형 모델에서의 정확도인 95%보다 조금 낮습니다.
결정 트리의 깊이를 제한하지 않으면 트리는 무한정 깊어지고 복잡해질 수 있습니다. 그래서 가지치기하지 않은 트리는 과대적합되기 쉽고 새로운 데이터에 잘 일반화되지 않습니다. 이제 사전 가지치기를 트리에 적용해서 훈련 데이터에 완전히 학습되기 전에 트리의 성장을 막아보겠습니다. 한 가지 방법은 일정 깊이에 도달하면 트리의 성장을 멈추게 하는 것입니다. max_depth=4 옵션을 주면 연속된 질문을 최대 4개로 제한합니다([그림 2-24]와 [그림 2-26]을 비교해보세요). 트리 깊이를 제한하면 과대적합이 줄어듭니다. 이는 훈련 세트의 정확도를 떨어뜨리지만 테스트 세트의 성능은 개선시킵니다.
In[60]:
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(tree.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(tree.score(X_test, y_test)))
Out[60]:
훈련 세트 정확도: 0.988 테스트 세트 정확도: 0.951
결정 트리 분석
트리 모듈의 export_graphviz 함수를 이용해 트리를 시각화할 수 있습니다. 이 함수는 그래프 저장용 텍스트 파일 포맷인 .dot 파일을 만듭니다. 각 노드에서 다수인 클래스를 색으로 나타내기 위해 옵션 3 을 주고 적절히 레이블되도록 클래스 이름과 특성 이름을 매개변수로 전달합니다.
In[61]:
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["악성", "양성"],
feature_names=cancer.feature_names,
impurity=False, filled=True)
이 파일을 읽어서 graphviz 모듈 4 을 사용해 [그림 2-27]처럼 시각화할 수 있습니다(또는 .dot 파일을 읽을 수 있는 다른 프로그램을 사용해도 됩니다).
In[62]:
import graphviz
with open("tree.dot") as f:
dot_graph = f.read()
display(graphviz.Source(dot_graph))

그림 2-27 유방암 데이터셋으로 만든 결정 트리
트리를 시각화하면 알고리즘의 예측이 어떻게 이뤄지는지 잘 이해할 수 있으며 비전문가에게 머신러닝 알고리즘을 설명하기에 좋습니다. 그러나 여기서 보듯이 깊이가 4만 되어도 트리는 매우 장황해집니다. 트리가 더 깊어지면(10 정도의 깊이는 보통입니다) 한눈에 보기가 힘들어집니다. 트리를 조사할 때는 많은 수의 데이터가 흐르는 경로를 찾아보면 좋습니다. [그림 2-27]의 각 노드에 적힌 samples는 각 노드에 있는 샘플의 수를 나타내며 value는 클래스당 샘플의 수를 제공합니다. 루트 노드의 오른쪽 가지를 따라가면(worst radius > 16.795) 악성 샘플이 134개, 양성 샘플이 8개인 노드를 만듭니다. 이 방향의 트리 나머지는 이 8개의 양성 샘플을 더 세부적으로 분리합니다. 첫 노드에서 오른쪽으로 분리된 142개 샘플 중 거의 대부분(132개)이 가장 오른쪽 노드로 갑니다.
루트 노드에서 왼쪽으로 간 데이터, 즉 worst radius <= 16.795인 데이터는 악성 샘플이 25개이고 양성 샘플이 259개입니다. 대부분의 양성 샘플은 왼쪽에서 두 번째 노드에 할당되고 나머지 리프 노드 대부분은 매우 적은 양의 샘플만 가지고 있습니다.
트리의 특성 중요도
전체 트리를 살펴보는 것은 어려울 수 있으니, 대신 트리가 어떻게 작동하는지 요약하는 속성들을 사용할 수 있습니다. 가장 널리 사용되는 속성은 트리를 만드는 결정에 각 특성이 얼마나 중요한지를 평가하는 특성 중요도feature importance입니다. 이 값은 0과 1 사이의 숫자로, 각 특성에 대해 0은 전혀 사용되지 않았다는 뜻이고 1은 완벽하게 타깃 클래스를 예측했다는 뜻입니다. 특성 중요도의 전체 합은 1입니다.
In[63]:
print("특성 중요도:\n{}".format(tree.feature_importances_))
Out[63]:
특성 중요도: [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.01 0.048 0. 0. 0.002 0. 0. 0. 0. 0. 0.727 0.046 0. 0. 0.014 0. 0.018 0.122 0.012 0. ]
선형 모델의 계수를 시각화하는 것과 비슷한 방법으로 특성 중요도도 시각화할 수 있습니다(그림 2-28).
In[64]:
def plot_feature_importances_cancer(model):
n_features = cancer.data.shape[1]
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), cancer.feature_names)
plt.xlabel("특성 중요도")
plt.ylabel("특성")
plt.ylim(-1, n_features)
plot_feature_importances_cancer(tree)

그림 2-28 유방암 데이터로 학습시킨 결정 트리의 특성 중요도
첫 번째 노드에서 사용한 특성(“worst radius”)이 가장 중요한 특성으로 나타납니다. 이 그래프는 첫 번째 노드에서 두 클래스를 꽤 잘 나누고 있다는 우리의 관찰을 뒷받침해줍니다.
그러나 어떤 특성의 feature_importance_ 값이 낮다고 해서 이 특성이 유용하지 않다는 뜻은 아닙니다. 단지 트리가 그 특성을 선택하지 않았을 뿐이며 다른 특성이 동일한 정보를 지니고 있어서일 수 있습니다.
선형 모델의 계수와는 달리, 특성 중요도는 항상 양수이며 특성이 어떤 클래스를 지지하는지는 알 수 없습니다. 즉 특성 중요도의 값은 “worst radius”가 중요하다고 알려주지만 높은 반지름이 양성을 의미하는지 악성을 의미하는지는 알 수 없습니다. 사실 특성과 클래스 사이에는 간단하지 않은 관계가 있을 수 있으며 다음 예에서 이런 점을 살펴보겠습니다(그림 2-29, 2-30).
In[65]:
tree = mglearn.plots.plot_tree_not_monotone() display(tree)
Out[65]:
Feature importances: [ 0. 1.]

그림 2-29 y 축의 특성이 클래스 레이블과 복합적인 관계를 가지고 있는 2차원 데이터셋과 결정 트리가 만든 결정 경계

그림 2-30 [그림 2-29]에 나타난 데이터로 학습한 결정 트리
이 그림은 두 개의 특성과 두 개의 클래스를 가진 데이터셋을 보여줍니다. X[1]에 있는 정보만 사용되었고 X[0]은 전혀 사용되지 않았습니다. 하지만 X[1]과 출력 클래스와의 관계는 단순하게 비례 또는 반비례하지 않습니다. 즉 “X[1] 값이 높으면 클래스 0이고 값이 낮으면 1”이라고(또는 그 반대로) 말할 수 없습니다.
우리는 여기서 결정 트리를 가지고 분류에 대해서만 논하고 있지만 여기에서 말한 것들은 DecisionTreeRegressor로 구현된 회귀 결정 트리에서도 비슷하게 적용됩니다. 회귀 트리의 사용법과 분석은 분류 트리와 매우 비슷합니다. 하지만 회귀를 위한 트리 기반의 모델을 사용할 때 짚고 넘어가야 할 특별한 속성이 하나 있습니다. DecisionTreeRegressor(그리고 모든 다른 트리 기반 회귀 모델)는 외삽extrapolation, 즉 훈련 데이터의 범위 밖의 포인트에 대해 예측을 할 수 없습니다.
컴퓨터 메모리 가격 동향 데이터셋을 이용해 더 자세히 살펴보겠습니다. [그림 2-31]의 x 축은 날짜, y 축은 해당 년도의 램(RAM) 1메가바이트당 가격입니다.
In[66]:
import pandas as pd
ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH, "ram_price.csv"))
plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("년")
plt.ylabel("가격 ($/Mbyte_")

그림 2-31 로그 스케일로 그린 램 가격 동향
y 축은 로그 스케일입니다. 그래프를 로그 스케일로 그리면 약간의 굴곡을 제외하고는 선형적으로 나타나서 비교적 예측하기가 쉬워집니다.
날짜 특성 하나만으로 2000년 전까지의 데이터로부터 2000년 후의 가격을 예측해보겠습니다. 여기서는 간단한 두 모델 DecisionTreeRegressor와 LinearRegression을 비교해보겠습니다. 가격을 로그 스케일로 바꾸었기 때문에 비교적 선형적인 관계를 가집니다. 로그 스케일로 바꾸어도 DecisionTreeRegressor를 사용하는 데는 아무런 차이가 없지만 LinearRegression에는 큰 차이가 있습니다(4장에서 자세히 다루겠습니다). 모델을 훈련시키고 예측을 수행한 다음 로그 스케일을 되돌리기 위해 지수 함수를 적용합니다. 그래프 표현을 위해 전체 데이터셋에 대해 예측을 수행하였지만 테스트 데이터셋과의 비교가 관심 대상입니다.
In[67]:
from sklearn.tree import DecisionTreeRegressor # 2000년 이전을 훈련 데이터로, 2000년 이후를 테스트 데이터로 만듭니다. data_train = ram_prices[ram_prices.date < 2000] data_test = ram_prices[ram_prices.date >= 2000] # 가격 예측을 위해 날짜 특성만을 이용합니다. X_train = data_train.date[:, np.newaxis] # 데이터와 타깃의 관계를 간단하게 만들기 위해 로그 스케일로 바꿉니다. y_train = np.log(data_train.price) tree = DecisionTreeRegressor().fit(X_train, y_train) linear_reg = LinearRegression().fit(X_train, y_train) # 예측은 전체 기간에 대해서 수행합니다. X_all = ram_prices.date[:, np.newaxis] pred_tree = tree.predict(X_all) pred_lr = linear_reg.predict(X_all) # 예측한 값의 로그 스케일을 되돌립니다. price_tree = np.exp(pred_tree) price_lr = np.exp(pred_lr)
[그림 2-32]는 실제 값과 결정 트리, 선형 회귀의 예측값을 비교한 것입니다.
In[68]:
plt.semilogy(data_train.date, data_train.price, label="훈련 데이터") plt.semilogy(data_test.date, data_test.price, label="테스트 데이터") plt.semilogy(ram_prices.date, price_tree, label="트리 예측") plt.semilogy(ram_prices.date, price_lr, label="선형 회귀 예측") plt.legend()

그림 2-32 램 가격 데이터를 사용해 만든 선형 모델과 회귀 트리의 예측값 비교
두 모델은 확연한 차이를 보입니다. 선형 모델은 우리가 아는 대로 직선으로 데이터를 근사하였습니다. 이 직선은 훈련 데이터와 테스트 데이터에 있는 미세한 굴곡을 매끈하게 근사하여 테스트 데이터(2000년 이후)를 꽤 정확히 예측합니다. 반면에 트리 모델은 훈련 데이터를 완벽하게 예측합니다. 트리의 복잡도에 제한을 두지 않아서 전체 데이터셋을 모두 기억하기 때문입니다. 그러나 모델이 가진 데이터 범위 밖으로 나가면 단순히 마지막 포인트를 이용해 예측하는 게 전부입니다. 트리 모델은 훈련 데이터 밖의 새로운 데이터를 예측할 능력이 없습니다. 이는 모든 트리 기반 모델의 공통된 단점입니다. 5
장단점과 매개변수
앞서 설명처럼 결정 트리에서 모델 복잡도를 조절하는 매개변수는 트리가 완전히 만들어지기 전에 멈추게 하는 사전 가지치기 매개변수입니다. 보통은 사전 가지치기 방법 중 max_depth, max_leaf_nodes 또는 min_samples_leaf 중 하나만 지정해도 과대적합을 막는 데 충분합니다. 6
결정 트리가 이전에 소개한 다른 알고리즘들보다 나은 점은 두 가지입니다. 첫째, 만들어진 모델을 쉽게 시각화할 수 있어서 비전문가도 이해하기 쉽습니다(비교적 작은 트리일 때). 그리고 데이터의 스케일에 구애받지 않습니다. 각 특성이 개별적으로 처리되어 데이터를 분할하는 데 데이터 스케일의 영향을 받지 않으므로 결정 트리에서는 특성의 정규화나 표준화 같은 전처리 과정이 필요 없습니다. 특히 특성의 스케일이 서로 다르거나 이진 특성과 연속적인 특성이 혼합되어 있을 때도 잘 작동합니다.
결정 트리의 주요 단점은 사전 가지치기를 사용함에도 불구하고 과대적합되는 경향이 있어 일반화 성능이 좋지 않다는 것입니다. 그래서 다음에 설명할 앙상블 방법을 단일 결정 트리의 대안으로 흔히 사용합니다.
–
–
- 옮긴이_ 원 모양이 클래스 0이고 삼각형 모양이 클래스 1의 데이터 포인트를 나타냅니다.
- 옮긴이_ 깃허브에 있는 주피터 노트북에서 전체 트리를 볼 수 있습니다.
- 옮긴이_ export_graphviz 함수에 filled 매개변수를 True로 지정하면 노드의 클래스가 구분되도록 색으로 칠해집니다.
- 옮긴이_ graphviz 모듈은 pip install graphviz 명령으로 설치할 수 있습니다. 주피터 노트북이 아닐 경우 graphviz.Source의 결과를 변수로 저장하여 pdf, png 등의 파일로 저장할 수 있습니다. dot=graphviz.Source(dot_graph); dot.format=’png’; dot.render(filename=’tree.png’)
- 사실 트리 기반 모델로 좋은 예측을 만들 수 있습니다(예를 들면 가격이 오르거나 내릴지를 예측할 때). 이 예제의 목적은 트리 모델이 시계열 데이터엔 잘 맞지 않는다는 것과 트리가 어떻게 예측을 만드는지 그 특성을 보여주기 위함입니다.
- 옮긴이_ max_leaf_nodes는 리프 노드의 최대 개수를 지정하는 매개변수이고 min_samples_leaf는 리프 노드가 되기 위한 최소한의 샘플 개수를 지정합니다. 이외에도 min_samples_split 매개변수를 사용하여 노드가 분기할 수 있는 최소 샘플 개수를 지정할 수 있습니다.
–
2.3.4 나이브 베이즈 분류기 | 목차 | 2.3.6 결정 트리의 앙상블
–

잘봤습니다~!
좋아요Liked by 2 people
In[62]:
import graphviz
with open(“tree.dot”) as f:
dot_graph = f.read()
display(graphviz.Source(dot_graph))
여기 부분에서 아래와 같은 오류가 납니다.
—————————————————————————
UnicodeDecodeError Traceback (most recent call last)
in ()
2
3 with open(“tree.dot”) as f:
—-> 4 dot_graph = f.read()
5 display(graphviz.Source(dot_graph))
UnicodeDecodeError: ‘cp949’ codec can’t decode byte 0xec in position 144: illegal multibyte sequence
좋아요좋아요
혹시 파이썬 2.x 를 쓰시나요? 아니면 윈도우즈 환경인 것 같군요. open(…, “rb”) 로 파일을 읽어 보시겠어요?
좋아요좋아요
그렇게 했는데도
CalledProcessError Traceback (most recent call last)
~\Anaconda3\lib\site-packages\IPython\core\formatters.py in __call__(self, obj)
343 method = get_real_method(obj, self.print_method)
344 if method is not None:
–> 345 return method()
346 return None
347 else:
~\Anaconda3\lib\site-packages\graphviz\files.py in _repr_svg_(self)
104
105 def _repr_svg_(self):
–> 106 return self.pipe(format=’svg’).decode(self._encoding)
107
108 def pipe(self, format=None):
~\Anaconda3\lib\site-packages\graphviz\files.py in pipe(self, format)
123 data = text_type(self.source).encode(self._encoding)
124
–> 125 outs = backend.pipe(self._engine, format, data)
126
127 return outs
~\Anaconda3\lib\site-packages\graphviz\backend.py in pipe(engine, format, data, quiet)
171 stderr_write_binary(errs)
172 sys.stderr.flush()
–> 173 raise subprocess.CalledProcessError(proc.returncode, args, output=outs)
174
175 return outs
CalledProcessError: Command ‘[‘dot.bat’, ‘-Tsvg’]’ returned non-zero exit status 1.
라는 에러가 뜨네요 어떻게 해야할까요?
도와주시면 감사하겠습니다.
좋아요좋아요
graphviz의 dot.bat 파일을 찾지 못해서 생기는 에러 같습니다. 혹시 conda 에서 graphviz를 설치했다면 지우고 pip install graphviz 로 설치해 보시겠어요?
좋아요좋아요
참고로
import graphviz
with open(“tree.dot”,”rb”) as f:
dot_graph = f.read()
display(graphviz.Source(dot_graph))
이렇게 입력했습니다.
좋아요좋아요
open(“tree.dot”, encoding=”utf-8″) 로 하시면 됩니다.
좋아요Liked by 1명
안녕하세요 박인구님, 답변 감사드립니다.
말씀하신대로 해보았더니
FileNotFoundError Traceback (most recent call last)
~\Anaconda3\lib\site-packages\graphviz\backend.py in pipe(engine, format, data, quiet)
158 stdout=subprocess.PIPE, stderr=subprocess.PIPE,
–> 159 **POPEN_KWARGS)
160 except OSError as e:
~\Anaconda3\lib\subprocess.py in __init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, encoding, errors)
708 errread, errwrite,
–> 709 restore_signals, start_new_session)
710 except:
~\Anaconda3\lib\subprocess.py in _execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, unused_restore_signals, unused_start_new_session)
996 os.fspath(cwd) if cwd is not None else None,
–> 997 startupinfo)
998 finally:
FileNotFoundError: [WinError 2] The system cannot find the file specified
During handling of the above exception, another exception occurred:
ExecutableNotFound Traceback (most recent call last)
~\Anaconda3\lib\site-packages\IPython\core\formatters.py in __call__(self, obj)
343 method = get_real_method(obj, self.print_method)
344 if method is not None:
–> 345 return method()
346 return None
347 else:
~\Anaconda3\lib\site-packages\graphviz\files.py in _repr_svg_(self)
104
105 def _repr_svg_(self):
–> 106 return self.pipe(format=’svg’).decode(self._encoding)
107
108 def pipe(self, format=None):
~\Anaconda3\lib\site-packages\graphviz\files.py in pipe(self, format)
123 data = text_type(self.source).encode(self._encoding)
124
–> 125 outs = backend.pipe(self._engine, format, data)
126
127 return outs
~\Anaconda3\lib\site-packages\graphviz\backend.py in pipe(engine, format, data, quiet)
160 except OSError as e:
161 if e.errno == errno.ENOENT:
–> 162 raise ExecutableNotFound(args)
163 else: # pragma: no cover
164 raise
ExecutableNotFound: failed to execute [‘dot’, ‘-Tsvg’], make sure the Graphviz executables are on your systems’ PATH
라는 에러가 뜨네요.
graphviz의 경로가 잘못되었다는 뜻 같은데 c:user\user\anaconda3\Lib\site-packages에는 graphviz가 잘 들어있네요. 뭐가 잘못된걸 까요?
좋아요좋아요
안녕하세요.
jupyter lab에서 65번 코드를 실행하려고 import mglearn을 했으나 ImportError: cannot import name ‘imread’에러가 발생합니다.
구글링을 해봤으나 도저히 해결책을 모르겠어서 문의 드립니다.
참고로 mglearn과 더불어 필요한 모듈의 버전은 다음과 같으며 전 virtualenv 가상환경에서 pip install로 mglearn을 설치 했습니다.
Name: numpy
Version: 1.14.2
Name: scipy
Version: 1.0.1
Name: scikit-learn
Version: 0.19.1
Name: matplotlib
Version: 2.2.2
Name: pandas
Version: 0.22.0
Name: Pillow
Version: 5.1.0
Name: graphviz
Version: 0.8.3
좋아요좋아요
안녕하세요. haesunrpark 지메일 계정으로 에러 메세지 전체를 보내 주시면 확인하기 좋을 것 같습니다.
좋아요좋아요
이번엔
FileNotFoundError Traceback (most recent call last)
~\Anaconda3\lib\site-packages\graphviz\backend.py in pipe(engine, format, data, quiet)
158 stdout=subprocess.PIPE, stderr=subprocess.PIPE,
–> 159 **POPEN_KWARGS)
160 except OSError as e:
~\Anaconda3\lib\subprocess.py in __init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, encoding, errors)
708 errread, errwrite,
–> 709 restore_signals, start_new_session)
710 except:
~\Anaconda3\lib\subprocess.py in _execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, unused_restore_signals, unused_start_new_session)
996 os.fspath(cwd) if cwd is not None else None,
–> 997 startupinfo)
998 finally:
FileNotFoundError: [WinError 2] 지정된 파일을 찾을 수 없습니다
During handling of the above exception, another exception occurred:
ExecutableNotFound Traceback (most recent call last)
~\Anaconda3\lib\site-packages\IPython\core\formatters.py in __call__(self, obj)
343 method = get_real_method(obj, self.print_method)
344 if method is not None:
–> 345 return method()
346 return None
347 else:
~\Anaconda3\lib\site-packages\graphviz\files.py in _repr_svg_(self)
104
105 def _repr_svg_(self):
–> 106 return self.pipe(format=’svg’).decode(self._encoding)
107
108 def pipe(self, format=None):
~\Anaconda3\lib\site-packages\graphviz\files.py in pipe(self, format)
123 data = text_type(self.source).encode(self._encoding)
124
–> 125 outs = backend.pipe(self._engine, format, data)
126
127 return outs
~\Anaconda3\lib\site-packages\graphviz\backend.py in pipe(engine, format, data, quiet)
160 except OSError as e:
161 if e.errno == errno.ENOENT:
–> 162 raise ExecutableNotFound(args)
163 else: # pragma: no cover
164 raise
ExecutableNotFound: failed to execute [‘dot’, ‘-Tsvg’], make sure the Graphviz executables are on your systems’ PATH
라고 뜨네요
좋아요좋아요
안녕하세요. 유사한 댓글을 계속 올리면 워드프레스에서 자동으로 스팸처리됩니다. 아마도 원인은 dot.bat 파일을 찾지 못하기 때문으로 보입니다. In[62] 코드를 ipython이나 python 쉘에서 시도해 보세요.
좋아요좋아요
‘cp949’ codec can’t decode byte 0xec in position 144: illegal multibyte sequence
라고 뜨네요.
좋아요좋아요
Ipython이나 python 쉘에서 open(…, ‘rb’) 로 바꾸어 실행해 보시겠어요?
좋아요좋아요
감사합니다.
오류없이 실행됩니다.
그런데 왜 ipython에서 트리가 표시되지 않는지,또 왜 주피터 노트북에서는 왜 안되는지 궁금합니다.
도움주시면 감사하겠습니다.
좋아요좋아요
쉘에서 이상없이 작동된다면 두 개 이상의 파이썬 배포판이 설치되어 있거나 콘다 환경이 여러 개일 수 있습니다. 이런 환경에서는 jupyter가 다른 파이썬 버전을 사용하는 경우가 종종 있습니다. 작업에 필요한 라이브러리가 적절한 파이썬 버전과 콘다 환경에 설치되어 있는지 확인해 보세요. display 함수는 노트북에서는 미려한 그림을 보여주지만 쉘에서는 그냥 print 함수와 비슷합니다.
좋아요좋아요
버젼은 잘 맞는데 말이죠…… 다른 방법은 없을까요?
좋아요좋아요
노트북과 쉘에서 파이썬과 임포트한 모듈의 경로를 다음 명령으로 확인해 보세요. import sys; print(sys.executable); import graphviz; print(graphviz.__path__)
좋아요좋아요
경로는 같다고 나옵니다.
좋아요좋아요
주피터 노트북과 ipython 쉘의 파이썬 경로가 같다면 두 환경에서 동작이 같아야 하는데요. 다른 이유를 모르겠네요. ㅠ.ㅠ
좋아요좋아요
import sys; print(sys.executable); import graphviz; print(graphviz.__path__) 로 했을때
아래와같이 두 환경이 같습니다…..
C:\ProgramData\Anaconda3\python.exe
[‘C:\\ProgramData\\Anaconda3\\lib\\site-packages\\graphviz’]
헌데…
import graphviz
with open(“tree.dot”) as f:
dot_graph = f.read()
display(graphviz.Source(dot_graph))
이 코드를 실행하면 오류가 납니다… ㅠ path 설정이 문제인가요 ?
—————————————————————————
FileNotFoundError Traceback (most recent call last)
C:\ProgramData\Anaconda3\lib\site-packages\graphviz\backend.py in run(cmd, input, capture_output, check, quiet, **kwargs)
110 try:
–> 111 proc = subprocess.Popen(cmd, **kwargs)
112 except OSError as e:
C:\ProgramData\Anaconda3\lib\subprocess.py in __init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, encoding, errors)
708 errread, errwrite,
–> 709 restore_signals, start_new_session)
710 except:
C:\ProgramData\Anaconda3\lib\subprocess.py in _execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, unused_restore_signals, unused_start_new_session)
996 os.fspath(cwd) if cwd is not None else None,
–> 997 startupinfo)
998 finally:
FileNotFoundError: [WinError 2] 지정된 파일을 찾을 수 없습니다
During handling of the above exception, another exception occurred:
ExecutableNotFound Traceback (most recent call last)
C:\ProgramData\Anaconda3\lib\site-packages\IPython\core\formatters.py in __call__(self, obj)
343 method = get_real_method(obj, self.print_method)
344 if method is not None:
–> 345 return method()
346 return None
347 else:
C:\ProgramData\Anaconda3\lib\site-packages\graphviz\files.py in _repr_svg_(self)
104
105 def _repr_svg_(self):
–> 106 return self.pipe(format=’svg’).decode(self._encoding)
107
108 def pipe(self, format=None):
C:\ProgramData\Anaconda3\lib\site-packages\graphviz\files.py in pipe(self, format)
123 data = text_type(self.source).encode(self._encoding)
124
–> 125 outs = backend.pipe(self._engine, format, data)
126
127 return outs
C:\ProgramData\Anaconda3\lib\site-packages\graphviz\backend.py in pipe(engine, format, data, quiet)
160 “””
161 cmd, _ = command(engine, format)
–> 162 out, _ = run(cmd, input=data, capture_output=True, check=True, quiet=quiet)
163 return out
164
C:\ProgramData\Anaconda3\lib\site-packages\graphviz\backend.py in run(cmd, input, capture_output, check, quiet, **kwargs)
112 except OSError as e:
113 if e.errno == errno.ENOENT:
–> 114 raise ExecutableNotFound(cmd)
115 else: # pragma: no cover
116 raise
ExecutableNotFound: failed to execute [‘dot’, ‘-Tsvg’], make sure the Graphviz executables are on your systems’ PATH
좋아요좋아요
코드 때문에 스팸처리가 되어 있었네요. 아마도 GraphViz를 설치하지 않아서 발생하는 문제같습니다. https://www.graphviz.org/download/ 에서 설치파일을 다운 받아 설치해 주세요.
좋아요좋아요
위에 윈도우 환경에서 graphviz dot파일 불러오는데 오류가 나시는 분들은 보세염
우선 class name을 악성, 약성을 다른 영어 단어로 바꾸세요.
한글에서 우선 오류가 나는 것 같구요.
pip, conda install graphviz 해주시고요.
https://stackoverflow.com/questions/49471867/installing-graphviz-for-use-with-python-3-on-windows-10?noredirect=1&lq=1
이거 참고하셔서 윈도우 환경변수 맞춰주면 주피터 노트북에서 동작하는 거 확인했습니다. ㅎㅎ
좋아요Liked by 1명
안녕하세요. 글 정말 잘 봤습니다. 좋은 자료 올려주셔서 감사합니다.
중학생들에게 결정 트리에 대해서 알려주려고 하는데
예시가 정말 좋네요. 혹시 출처를 밝히고 멘토링할 때 사용해도 될까요?
좋아요좋아요
그럼요. 괜찮습니다 ^^
좋아요좋아요
이렇게 좋은 글 올려주셔서 감사드립니다. 많은 도움이 됐습니다. 공부 기록용으로 쓰고 있는 개인블로그가 있는데 본 포스트를 참고해서 글을 써도 될까요?
감사합니다
좋아요좋아요
네, 출처를 밝히시고 요약하시는 것은 괜찮습니다. 🙂
좋아요좋아요
display(graphviz.Source(dot_graph))
이 코드가 동작하지 않는 분들은
import IPython.display import display를 실행하고 해보시기 바랍니다.
좋아요Liked by 1명
from IPython.display import display
좋아요좋아요