합성곱^convolution 혹은 콘볼루션 신경망은 주로 시각 분야 애플리케이션에 널리 사용됩니다. 위키피디아의 합성곱 정의를 보면 “하나의 함수와 또 다른 함수를 반전 이동한 값을 곱한 다음, 구간에 대해 적분하여 새로운 함수를 구하는 수학 연산자이다“라고 잘 설명되어 있습니다. 그리고 다음과 같은 애니메이션으로도 많이 익숙합니다.

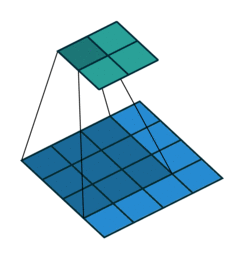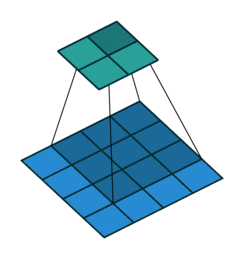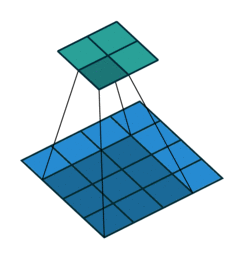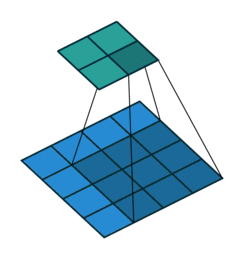
조금 더 적분스러운 표현의 그림은 위키피디아의 그림이 직관적입니다.

그림으로 표현이 어려운 점은 두 함수 중 하나를 반전시킨다는 점입니다.

합성곱과 거의 비슷한 연산으로 교차상관^{cross-correlation}이 있습니다. 교차상관의 정의를 보면 한 함수를 반전한다는 것만 빼고는 합성곱과 동일합니다.

합성곱:

교차상관:

합성곱 신경망의 입력값에 필터(가중치 혹은 커널)를 콘볼루션하려면 필터를 뒤집어서 적용해야 합니다. 그런데 어차피 필터의 값을 학습하려는 것이 목적이기 때문에 뒤집어서 콘볼루션을 하나 그냥 하나 동일합니다. 학습과 추론^inference시에 필터만 일정하면 됩니다. 그래서 딥러닝 프레임워크들은 합성곱이 아니고 그냥 교차상관으로 구현되어 있습니다. 하지만 관습상 합성곱이라고 부릅니다. 사실 이게 중요한 문제는 아닌 것 같습니다.

인기를 끌었던 “파이썬 머신 러닝” 2판이 나오면서 합성곱에 대한 내용이 많이 보강되었습니다. 보통 다른 책들은 피드포워드 신경망(혹은 퍼셉트론) 정도를 넘파이^NumPy로 직접 구현해 보고 합성곱 신경망부터는 텐서플로 같은 라이브러리를 사용하는 것이 일반적입니다. 합성곱이나 패딩, 스트라이드 등을 코드로 구현하기가 번거롭기 때문이겠죠.

여기서 저자는 직접 합성곱을 구현한 코드를 추가했습니다. 그런데 교차상관이 아니라 (필터를 뒤집어서) 진짜 합성곱을 했습니다. 물론 합성곱과 교차상관에 대한 비슷한 점을 언급하기는 했지만 굳이 합성곱을 구현할 필요가 있었을까, 보통의 경우 교차상관을 사용한다고 언급해주면 좋지 않았을까 하는 생각이 들었습니다. 그래서 메일을 보냈더니 다음 중쇄할 때 관련 코멘트를 추가한다고 회신이 왔네요.

혹시 원서를 읽으시는 분이 있다면 다른 라이브러리들이 진짜 합성곱 연산을 하는 것으로 오해하지 마세요. 🙂